九年级数学中考冲刺---相似三角形复习课件北师大版 课件VIP免费

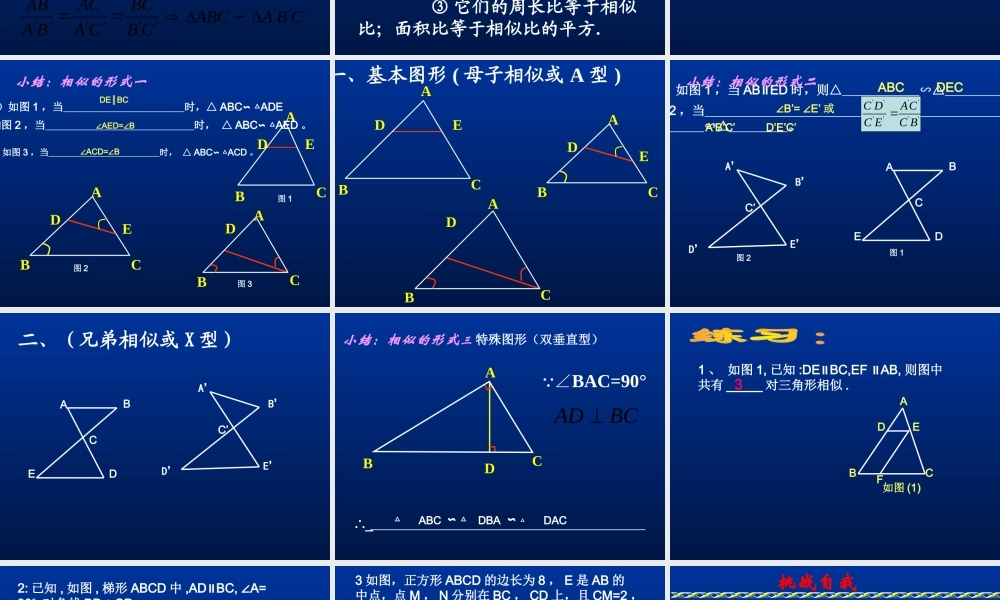
1. 相似三角形的定义：对应角相等、对应边成比例的三角形叫做相似三角形。2. 相似比：相似三角形的对应边的比，叫做相似三角形的相似比。 △ABC∽△A/B/C/, 如果 BC=3,B/C/=1.5, 那么△ A/B/C/与 △ ABC 的相似比为 _________. (1) 识别ABCCAB ①如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似．CBAABC∽BBAA ②如果一个三角形的两条边分别与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．ABCCABCBAABC∽AACAACBAAB ③如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形相似．ABCCABCBAABC∽CBBCCAACBAAB (2) 性质两个三角形相似，则 ③ 它们的周长比等于相似比；面积比等于相似比的平方． ① 它们的对应边成比例，对应角相等； ② 它们的对应高、对应中线、对应角平分线的比等于相似比； 应用举例例 1 判断① 所有的等腰三角形都相似．② 所有的直角三角形都相似．③ 所有的等边三角形都相似．④ 所有的等腰直角三角形都相似．(×)(√)(√)(×) 小结：相似的形式一（ 1 ）如图 1 ，当 时，△ ABC ADE∽ △ABCDE图 1 （ 2 ）如图 2 ，当 时， △ ABC AED∽ △。ABCDE图 2（ 3 ）如图 3 ，当 时， △ ABC ACD∽ △。ABCD图 3DE BC∥∠AED= B∠∠ACD= B∠ 一、基本图形 ( 母子相似或 A 型 )ABCDEABCDABCDE （ 1 ）如图 1 ，当 AB ED∥时，则△ ∽△ 。（ 2 ）如图 2 ，当 时，则△ ∽△ 。ABCDE图 1A’B’C’D’E’图 2ABC DEC∠B’= E’∠或''''''''C DACC EC BA’B’C’ D’E’C’小结：相似的形式二 二、（兄弟相似或 X 型）ABCDEA’B’C’D’E’ ABCDBCAD  ∠BAC=90°∴ △ ∽ △ ∽ △ABC DBA DAC小结：相似的形式三 特殊图形（双垂直型） 1 、 如图 1, 已知 :DE BC,EF AB,∥∥则图中共有 _____ 对三角形相似 .3ABCDEF如图 (1) 2: 已知 , 如图 , 梯形 ABCD 中 ,AD BC, A=∥∠900, 对角线 BDCD⊥求证 :(1) ABDDCB;△∽△ (2)BD2=AD·BCABCD证明 :(1) AD BC, ∥ ∴ ∠ADB= DBC∠ ∠A= BDC= 90°,∠ ∴ △ABDDCB∽△(2) ABDDCB △∽△∴AD = BD BD BC即...