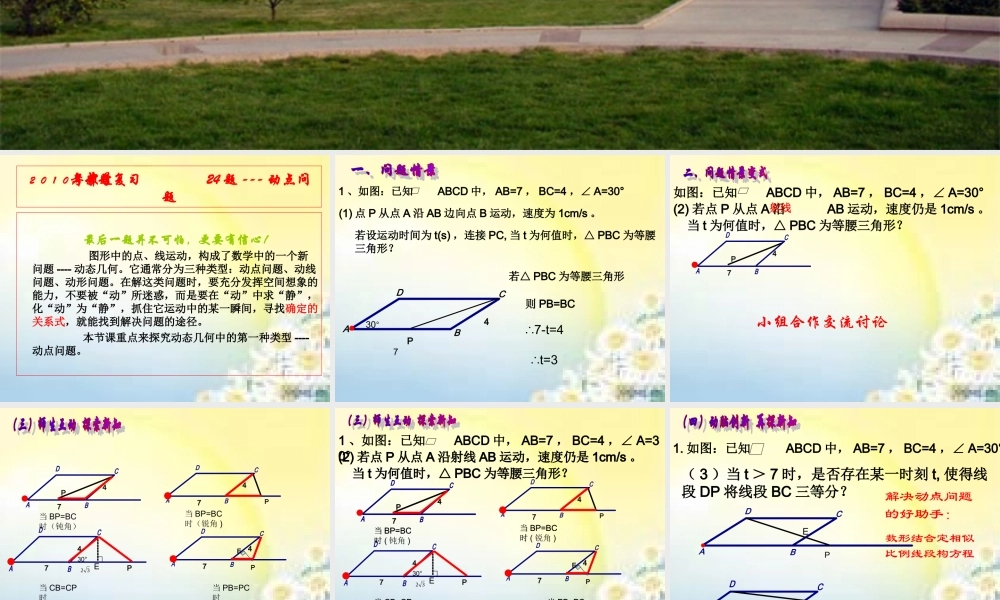
动 点 问 题 探 究山东省隐珠办事处中学 2010年中考数学专题复习24 题 --- 动点问题 最后一题并不可怕,更要有信心! 图形中的点、线运动,构成了数学中的一个新问题 ---- 动态几何。它通常分为三种类型:动点问题、动线问题、动形问题。在解这类问题时,要充分发挥空间想象的能力,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。 本节课重点来探究动态几何中的第一种类型 ----动点问题。 1 、如图:已知 ABCD 中, AB=7 , BC=4 ,∠ A=30°DCBA(1) 点 P 从点 A 沿 AB 边向点 B 运动,速度为 1cm/s 。7430°P若设运动时间为 t(s) ,连接 PC, 当 t 为何值时,△ PBC 为等腰三角形?若△ PBC 为等腰三角形则 PB=BC∴7-t=4∴t=3 如图:已知 ABCD 中, AB=7 , BC=4 ,∠ A=30°(2) 若点 P 从点 A 沿 AB 运动,速度仍是 1cm/s 。当 t 为何值时,△ PBC 为等腰三角形?PDCBA74射线小组合作交流讨论 PDCBA74当 BP=BC时(锐角 )PDCBA7430°当 CB=CP时∟E32P当 PB=PC时DCBA74PEDCBA74当 BP=BC时(钝角) 1 、如图:已知 ABCD 中, AB=7 , BC=4 ,∠ A=30°PDCBA74当 BP=BC时PDCBA7430°当 CB=CP时∟E32P当 PB=PC时DCBA74PEDCBA74当 BP=BC时(2) 若点 P 从点 A 沿射线 AB 运动,速度仍是 1cm/s 。当 t 为何值时,△ PBC 为等腰三角形?探究动点关键:化动为静,分类讨论,关注全过程(2) 若点 P 从点 A 沿射线 AB 运动,速度仍是 1cm/s 。当 t 为何值时,△ PBC 为等腰三角形?PDCBA74当 BP=BC时 ( 钝角 )当 BP=BC时 ( 锐角 )当 CB=CP时当 PB=PC时∴t=3 或 11 或 7+ 或 /3 时 △ PBC 为等腰三角形3434 1. 如图:已知 ABCD 中, AB=7 , BC=4 ,∠ A=30°DCBA( 3 )当 t > 7 时,是否存在某一时刻 t, 使得线段 DP 将线段 BC 三等分?PEPEDCBA解决动点问题的好助手:数形结合定相似比例线段构方程 2. 在 Rt ABC△中,∠ C=90° , AC=6cm , BC=8cm,点 P 由点 A 出发 ,沿 AC 向 C 匀速运动,速度为 2cm/s ,同时 CBAP点 Q 由 AB 中点 D 出发,沿 DB 向 B 匀速运动,速度为 1cm/s ,DQ连接 PQ ,若设运动时间为 t(s) (0 < t ≤3)( 1 )当 t 为何值...