九年级数学下册 第2章二次函数 22 二次函数的图象与性质第2课时教学课件 湘教版 课件VIP免费

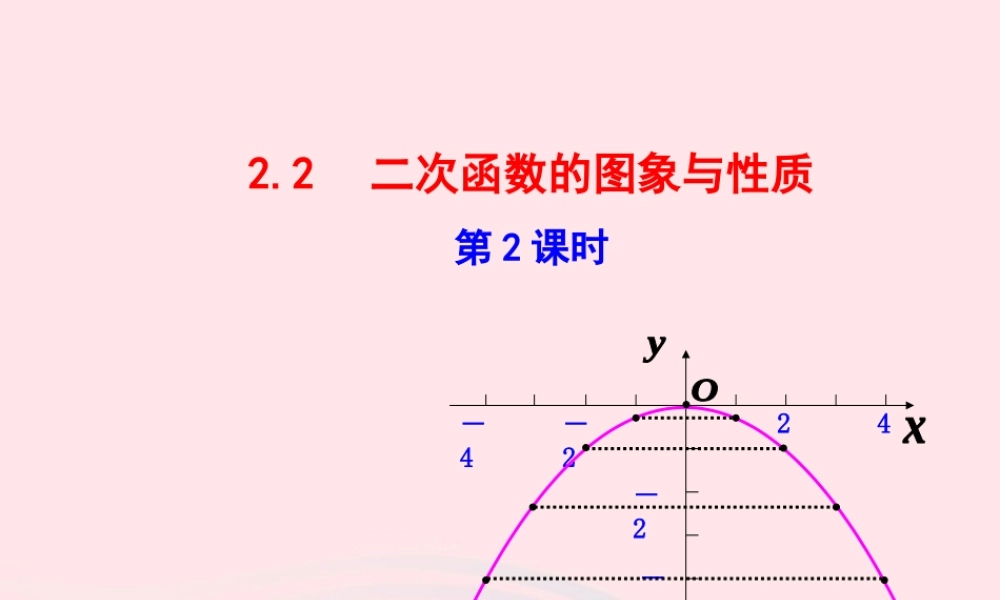
2.2 二次函数的图象与性质第 2 课时－2－424－2－41. 经历探索二次函数 y=ax2 的图象的作法和性质的过程，获得利用图象研究函数性质的经验 .2. 能够利用描点法作出 y=ax2 的图象，并能根据图象认识和理解二次函数 y=ax2 的性质 .3. 能够作出二次函数 y=ax2(a>0) 的图象，并能比较它与y=ax2(a<0) 的图象的异同，初步建立二次函数表达式与图象间的联系 .1. 二次函数的定义 一般地，形如 y=ax2+bx+c （ a ， b ， c 是常数， a≠0 ）的函数叫做 x 的二次函数 .2. 画函数图象的主要步骤是什么？（ 1 ）列表 .（ 3 ）连线 .（ 2 ）描点 .3. 请你画出二次函数 y=x2 的图象 .列表：yx… － 3 － 2 － 1 0 1 2 3 …… 9 4 1 0 1 4 9 … xyoy=x2 函数 y=x2 的图象是一条抛物线，它开口向上，图象是轴对称图形且关于 y轴对称 . 对称轴与抛物线的交点是抛物线的顶点，它是图象的最低点 .我们已经画出了 的图象，能不能从它得出二次函数 的图象呢？212yx212yx212yx212yx24－2－424－2－4PQ1. 在 的图象上任取一点 P （ ），它关于 x 轴的对称点 Q 的坐标是（ ）21,2aa212yx21, 2aa2. 点 Q 的坐标是否在 的图象上？ 212yx【探究】3. 由此可知，的图象与的图象关于 对称212yx212yx212yx212yx24－2－424－2－4PQx 轴4. 你怎样得到 的图象？212yx只要把 的图象沿着 x 轴翻折将图象“复印”下来，就得到 的图象了 .212yx212yx1. 对称轴是 __________ ，对称轴与图象的交点是____________; 图象的开口向 ___________.2. 图象在对称轴右边的部分，函数值随自变量取值的增大而 ____________ ，简称为右 ______________.3. 图象在对称轴左边的部分，函数值随自变量取值的增大而 ____________ ，简称为左 ______________.4. 当 x=__________ 时，函数值最 _____________.我们已经正确地画出了的图象，因此现在可以从图象看出的性质：212yx212yxy 轴下O （ 0 ，0 ）减小降增大升0大当 a<0 时， 的图象也具有上述性质，于是今后在画 的图象时，可以直接先画出图象在 y 轴右边的部分，然后利用对称性，画出图象在 y 轴左边的部分，在画右边部分时，只要“列表、描点、连线”三个步骤就可以了 . 2yax2yax (a0)【规律方法】例 . 画二次函数的图象 .214yxx012340－...