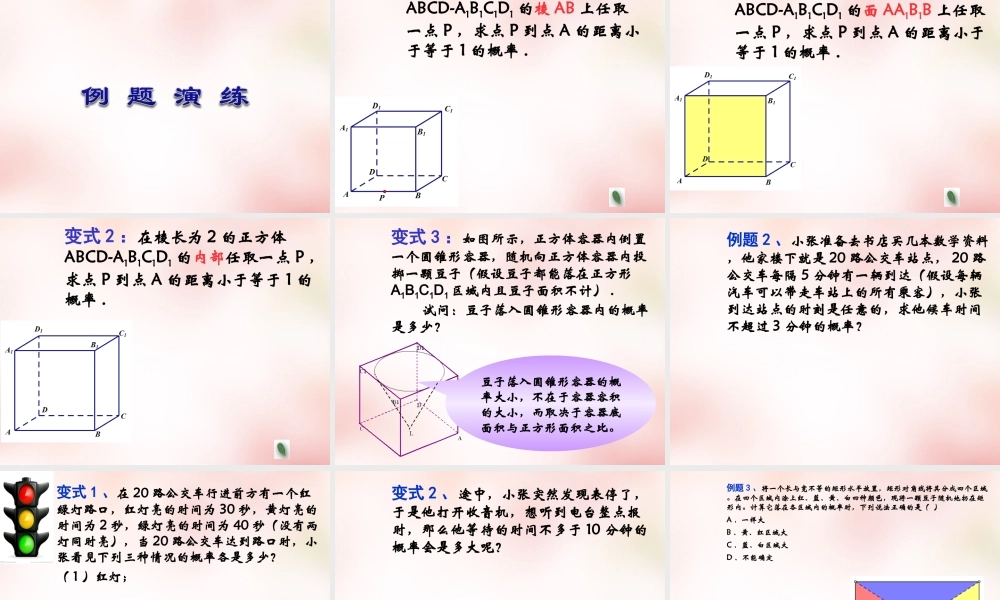
3.3 几何概型Ready?1 、下列概率模型中,几何概型的个数为( )① 某人在一串 10 把不同的钥匙中随意取一把,求一次就将门锁打开的概率;② 在圆心角为 90° 的扇形 AOB 中,以圆心 O为起点作射线 OC ,求使得∠ AOC 和∠ BOC都不小于 30° 的概率;③ 从 1,2,3,4 四个数中,任取两个数,求所取两数之一是 2 的概率;④ 一条海豚在水池中自由游戏,水池长 300m 、宽 20m 、深 10 米,求此海豚嘴尖离池壁不超过2m 的概率。 A 、 1 个 B 、 2 个 C 、 3 个 D 、 4 个2 、在 400 毫升自来水中有一个大肠杆菌,今从中随机取出 2 毫升水样放到显微镜下观察,则发现大肠杆菌的概率为( ) A 、 0.008 B 、 0.004 C 、 0.002 D 、 0.005EDCBA3 、如图,矩形 ABCD 中,点 E 为边 CD 的中点,若在矩形 ABCD 内部随机取一个点 Q ,则点 Q 取自△ ABE 内部的概率等于 ( )4 、在长为 12 cm 的线段 AB 上任取一点 M ,并以线段 AM 为边作正方形,则这个正方形的面积介于 36 cm2 与 81 cm2 之间的概率为( )5 、已知正方体 ABCD-A1B1C1D1 内有一个内切球 O ,则在正方体内任取点 M ,点 M 在球 O 内的概率是( )6 、如图,边长为 2 的正方形内有一不规则阴影部分,随机向正方形内投入 200 粒芝麻,恰有 60 粒落入阴影部分,则不规则图形的面积为( ) A 、 0.6 B 、 0.8 C 、 1.2 D 、1.5例题 1 :在棱长为 2 的正方体ABCD-A1B1C1D1 的棱 AB 上任取一点 P ,求点 P 到点 A 的距离小于等于 1 的概率 . 变式 1 :在棱长为 2 的正方体ABCD-A1B1C1D1 的面 AA1B1B 上任取一点 P ,求点 P 到点 A 的距离小于等于 1 的概率 .变式 2 :在棱长为 2 的正方体ABCD-A1B1C1D1 的内部任取一点 P ,求点 P 到点 A 的距离小于等于 1 的概率 . 变式 3 :如图所示,正方体容器内倒置一个圆锥形容器,随机向正方体容器内投掷一颗豆子(假设豆子都能落在正方形A1B1C1D1区域内且豆子面积不计) . 试问:豆子落入圆锥形容器内的概率是多少?豆子落入圆锥形容器的概率大小,不在于容器容积的大小,而取决于容器底面积与正方形面积之比。例题 2 、小张准备去书店买几本数学资料,他家楼下就是 20 路公交车站点, 20 路公交车每隔 5 分钟有一辆到达(假设每辆汽车可以带走车站上的所...