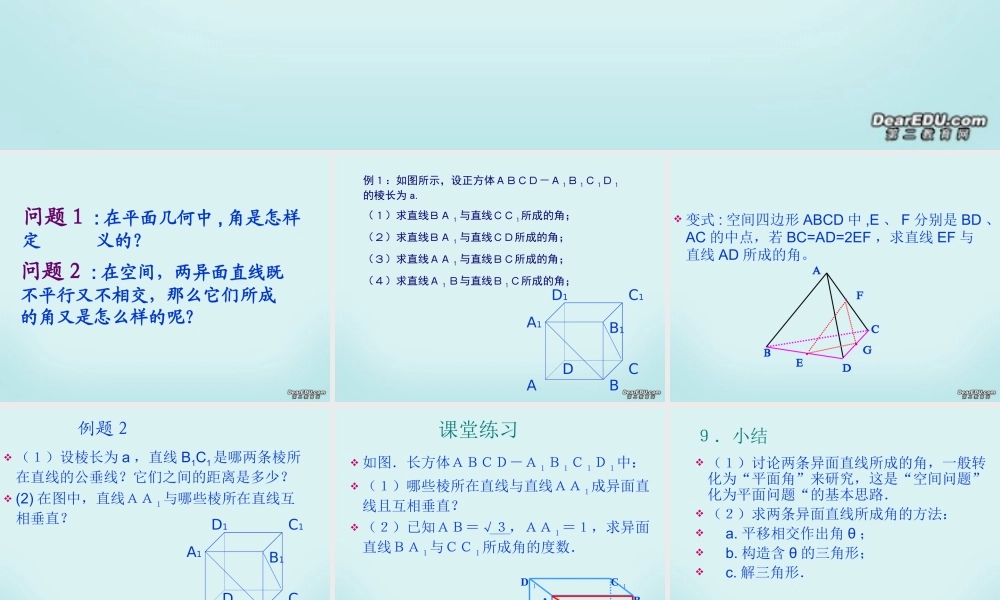
两条异面直线所成的角问题1 : 在平面几何中 , 角是怎样定 义的? 问题2 : 在空间,两异面直线既不平行又不相交,那么它们所成的角又是怎么样的呢?ABCDA1B1C1D1例1:如图所示,设正方体ABCD-A1B1C1D1的棱长为 a.(1)求直线BA 1 与直线CC1所成的角;(2)求直线BA 1 与直线CD所成的角;(3)求直线AA 1 与直线BC所成的角;(4)求直线A 1 B与直线B1C所成的角; 变式 : 空间四边形 ABCD 中 ,E 、 F 分别是 BD 、AC 的中点,若 BC=AD=2EF ,求直线 EF 与直线 AD 所成的角。ABCDE·FG·· (1)设棱长为 a ,直线 B1C1是哪两条棱所在直线的公垂线?它们之间的距离是多少? (2) 在图中,直线AA1与哪些棱所在直线互相垂直?ABCDA1B1C1D1例题2课堂练习 如图.长方体ABCD-A1B1C1D1中: (1)哪些棱所在直线与直线AA1成异面直线且互相垂直? (2)已知AB=√3,AA1=1,求异面直线BA1与CC1所成角的度数.ABCDA 1B 1C 1D 19.小结 (1)讨论两条异面直线所成的角,一般转化为“平面角”来研究,这是“空间问题”化为平面问题“的基本思路. (2)求两条异面直线所成角的方法: a. 平移相交作出角 θ ; b. 构造含 θ 的三角形; c. 解三角形.