中学七年级数学上册(3.2 解一元一次方程(一)—合并同类项与移项)课件1 (新版)新人教版 课件VIP免费

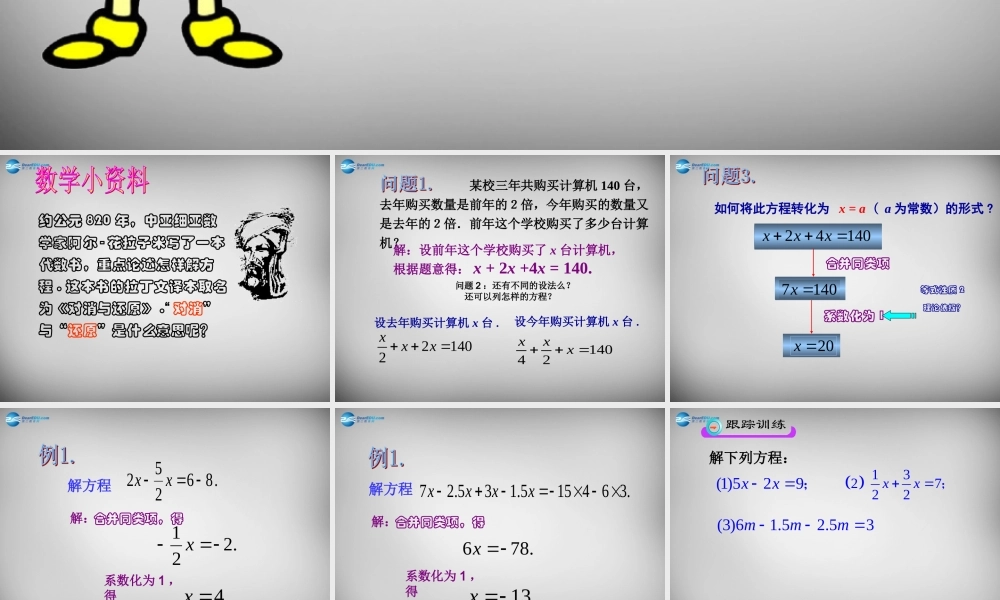
3.2 合并同类项与移项 (1)第三章 一元一次方程约公元 820 年，中亚细亚数学家阿尔 - 花拉子米写了一本代数书，重点论述怎样解方程 . 这本书的拉丁文译本取名为《对消与还原》 .“ 对消”与“还原”是什么意思呢？ 某校三年共购买计算机 140 台，去年购买数量是前年的２倍，今年购买的数量又是去年的２倍．前年这个学校购买了多少台计算机？解：设前年这个学校购买了 x 台计算机，根据题意得： x + 2x +4x = 140.设去年购买计算机 x 台 .设今年购买计算机 x 台 .21402xxx14042xxx问题 2 ：还有不同的设法么？还可以列怎样的方程？24140xxx1407 x20x如何将此方程转化为 x = a （ a 为常数）的形式 ?合并同类项系数化为 1等式性质 2理论依据？合并同类项，得系数化为 1 ，得. 86252xx解方程解：.221x.4x合并同类项，得系数化为 1 ，得.364155.135.27xxxx解方程解：.786x.13x  132722 ；xx(1)529 ；xx解下列方程：(3)61.52.53mmm1. 解方程：(1)30.510;xx(2)342520yy2. 洗衣厂今年计划生产洗衣机 25 500 台 ,其中Ⅰ型 ,Ⅱ 型 ,Ⅲ 型三种洗衣机的数量之比为 1:2:14, 这三种洗衣机计划各生产多少台 ?21425 500xxx解 : 设Ⅰ型 x 台，Ⅱ型 台 ,Ⅲ 型 台，则：2x14x 答：Ⅰ型 1 500 台 ,Ⅱ 型 3 000 台 ,Ⅲ 型 21 000 台 .合并同类项，得 17x=25 500系数化为 1 ，得 x=15003. 在遗留下来的古埃及草卷中 , 记载着一些数学问题 . 其中一个翻译过来就是“啊哈 , 它的全部 , 它的七分之一， 其和等于 19”. 你能求出问题中的“它”吗？请你根据题意列出方程 .4. 太阳下山晚霞红，我把鸭子赶回笼；一半在外闹哄哄，一半的一半进笼中；剩下十五围着我，共有多少请算清 .你能列出方程来解决这个问题吗？1. 今天学习的解方程有哪些步骤？2. 合并同类项在解方程的过程中起到了什么作用？驶向胜利的彼岸 合并同类项的目的就是化简方程，它是一种恒等变形，可以使方程变得简单，并逐步使方程向 x =a 的形式转化 ．合并同类项的作用：补充作业(1) 三个连续整数之和为 36. 求：这三个整数分别是多少？(2) 某科技兴趣小组共 32 人，其中男生与女生的人数之比为 3 ： 5 ，问男、女生各有多少人？