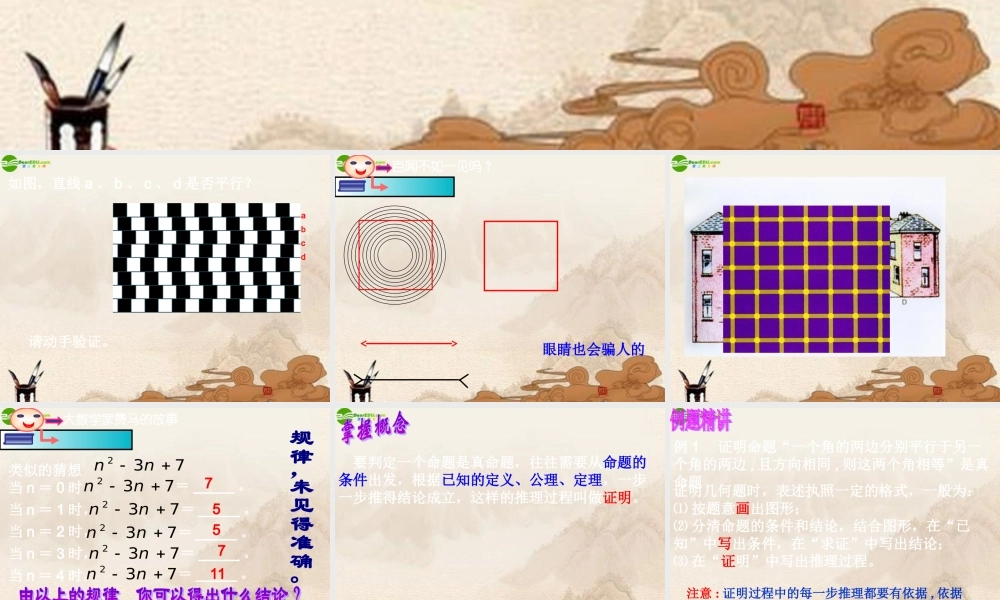
abcd如图,直线 a 、 b 、 c 、 d 是否平行?请动手验证。百闻不如一见吗?眼睛也会骗人的大数学家费马的故事237nn类似的猜想当 n = 0 时当 n = 1 时,当 n = 2 时,当 n = 3 时,当 n = 4 时,237nn= _____ 。7557237nn= _____ 。237nn= _____ 。237nn= _____ 。237nn= _____ 。11237nn= _____ 。当 n = 6 时,25 要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、公理、定理,一步一步推得结论成立,这样的推理过程叫做证明。例 1 证明命题“一个角的两边分别平行于另一个角的两边 , 且方向相同 , 则这两个角相等”是真命题 .证明几何题时,表述执照一定的格式,一般为:⑴ 按题意画出图形;⑵ 分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;⑶ 在“证明”中写出推理过程。注意 : 证明过程中的每一步推理都要有依据 , 依据作为推理的理由 , 可以写在每一步后的括号内 . 证明命题“两条直线被第三条直线所截,如果内错角相等,那么同位角也相等”是真命题。相信自己行,你就行!相信自己行,你就行!已知 : 如图 , AC 与 BD 交于点O,AO=CO,BO=DO . 求证 :AB CD .∥ABCDO 注意 : 如果给出的几何命题已包括了相应的图形、已知及求证,则可在表述时直接写出证明的推理过程.• 严格性之于数学家 , 犹如道德之于人 .• 由“因”导“果” , 执“果”索“因”是探索证明思路最基本的方法 .• 言必有据 , 因果对应 . 是初学证明者谨记和遵循的原则 .• 我们必须用科学的观点来看待一切事物 .本节课你学到什么?