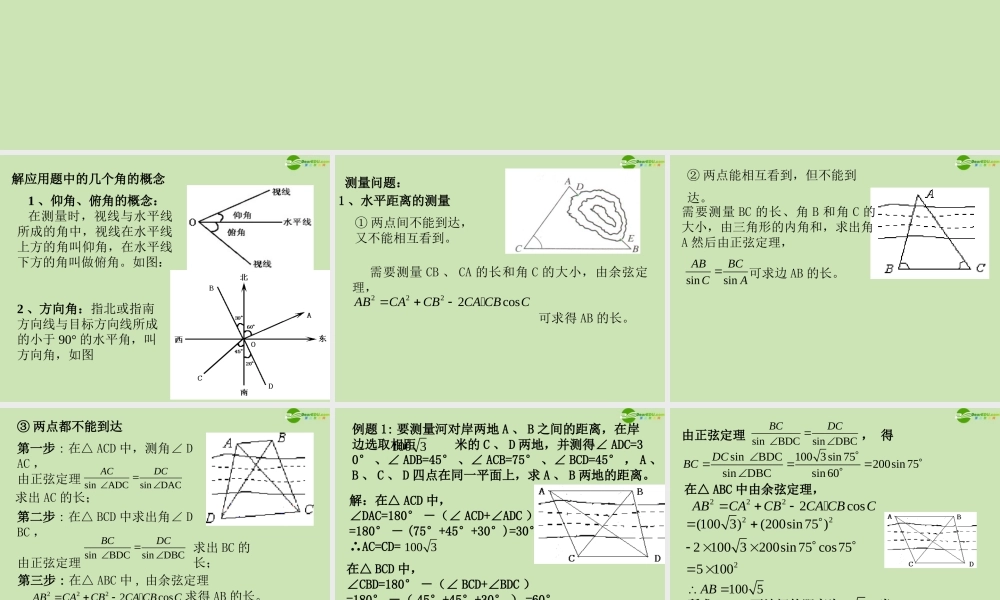
1.2 应用举例 课件 解应用题中的几个角的概念1 、仰角、俯角的概念:在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2 、方向角:指北或指南方向线与目标方向线所成的小于 90° 的水平角,叫方向角,如图 测量问题:1 、水平距离的测量① 两点间不能到达,又不能相互看到。 需要测量 CB 、 CA 的长和角 C 的大小,由余弦定理, 可求得 AB 的长。 2222cosABCACBCA CBC ② 两点能相互看到,但不能到达。 需要测量 BC 的长、角 B 和角 C 的大小,由三角形的内角和,求出角A 然后由正弦定理, 可求边 AB 的长。sinsinABBCCA ③ 两点都不能到达第一步 : 在△ ACD 中,测角∠ DAC ,由正弦定理 sin ADCsinDACACDC求出 AC 的长; 第二步 : 在△ BCD 中求出角∠ DBC ,由正弦定理 sin BDCsinDBCBCDC求出 BC 的长; 第三步 : 在△ ABC 中 , 由余弦定理 2222cosABCACBCA CBC求得 AB 的长。 例题 1: 要测量河对岸两地 A 、 B 之间的距离,在岸边选取相距 米的 C 、 D 两地,并测得∠ ADC=30° 、∠ ADB=45° 、∠ ACB=75° 、∠ BCD=45° , A 、B 、 C 、 D 四点在同一平面上,求 A 、 B 两地的距离。 100 3解:在△ ACD 中,∠DAC=180° -(∠ ACD+∠ADC )=180° - (75°+45°+30°)=30°∴AC=CD= 100 3在△ BCD 中,∠CBD=180° -(∠ BCD+∠BDC )=180° -( 45°+45°+30° ) =60° 由正弦定理 , 得sin BDCsinDBCBCDCsin BDC100 3sin 75200sin 75sinDBCsin 60DCBC在△ ABC 中由余弦定理, 2222cosABCACBCA CBC222(100 3)(200sin75 )2 100 3200sin75 cos755 100 100 5AB ∴所求 A 、 B 两地间的距离为 米。 100 5 测量垂直高度 1 、底部可以到达的; 测量出角 C 和 BC 的长度,解直角三角形即可求出 AB 的长。 2 、底部不能到达的 测量边 CD ,测量∠ C 和∠ ADB , cotcotCDABCADB 例题 2 :在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高 米,求山高 。BA60 CA45 BC32CD解:在△ ABC 中,∠ ABC=30° ,∠ACB =135° ,∴∠CAB =180° - (∠...