九年级数学上册 二次根式单元复习课件 人教新课标版 课件VIP免费

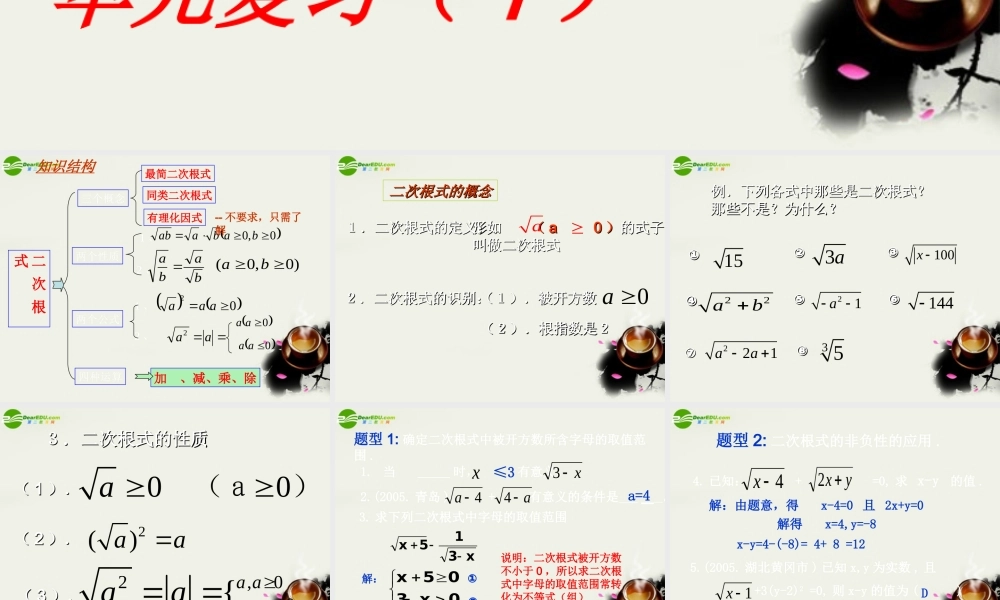
人教新版九年级上第 21 章 二 次 根 式单元复习（ 1 ） 二 次 根 式三个概念两个性质两个公式四种运算最简二次根式同类二次根式有理化因式baba )0,0(ba0,0babaab1 、2 、加 、减、乘、除知识结构2 、1 、 02aaaaa2 0aa0aa-- 不要求，只需了解二次根式的概念二次根式的概念形如 形如 （（ aa 00 ））的式子的式子叫做二次根式叫做二次根式a１．二次根式的定义：１．二次根式的定义：２．二次根式的识别：２．二次根式的识别：（１）．被开方数（１）．被开方数（２）．根指数是２（２）．根指数是２0a 例．下列各式中那些是二次根式？例．下列各式中那些是二次根式？那些不是？为什么？那些不是？为什么？153a100x 3 522ab21a144221aa⑧⑧⑦⑦⑥⑥⑤⑤④④①①②②③③３．二次根式的性质３．二次根式的性质（（ 11 ）．）．00a  （ａ）（（ 22 ）．）．2()aa（（ 33 ）．）．2,0,0{a aa aaa题型 1: 确定二次根式中被开方数所含字母的取值范围 .1. 当 _____ 时， 有意义。xx32.(2005. 青岛 ) +a4 3. 求下列二次根式中字母的取值范围x315x解得 - 5≤x ＜ 3解： 0x-305x①②说明：二次根式被开方数不小于 0 ，所以求二次根式中字母的取值范围常转化为不等式（组） ≤3a=44a有意义的条件是 __ .题型 2: 二次根式的非负性的应用 .4. 已知： + =0, 求 x-y 的值 .yx 24x5.(2005. 湖北黄冈市 ) 已知 x,y 为实数 , 且 +3(y-2)2 =0, 则 x-y 的值为 ( ) A.3 B.-3 C.1 D.-11x解：由题意，得 x-4=0 且 2x+y=0解得 x=4,y=-8x-y=4-(-8)= 4+ 8 =12D练 习抢答 : 判断下列二次根式是否是最简二次根式 , 并说明理由。621)6())(()5(75.0)4()3()2(50)1(2222babayxbca满足下列两个条件的二次根式 , 叫做最简二次根式（ 1 ）被开方数的因数是整数，因式是整式（ 2 ）被开方数中不含能开得尽方的因数或因式化简二次根式的方法：（ 1 ）如果被开方数是整数或整式时，先因数分解或因式分解 , 然后利用积的算术平方根的性质 , 将式子化简。（ 2 ）如果被开方数是分数或分式时 , 先利用商的算术平方根的性质 , 将其变为二次根式相除的形式 , 然后利用分母有理化 , 将式子化简。例 1 ：把下列各式化成最简二次根式22164...