九年级数学下册 第27章二次函数272二次函数的图象与性质 2二次函数yax2bxc的图象与性质(第2课时)课件 华东师大版 课件VIP免费

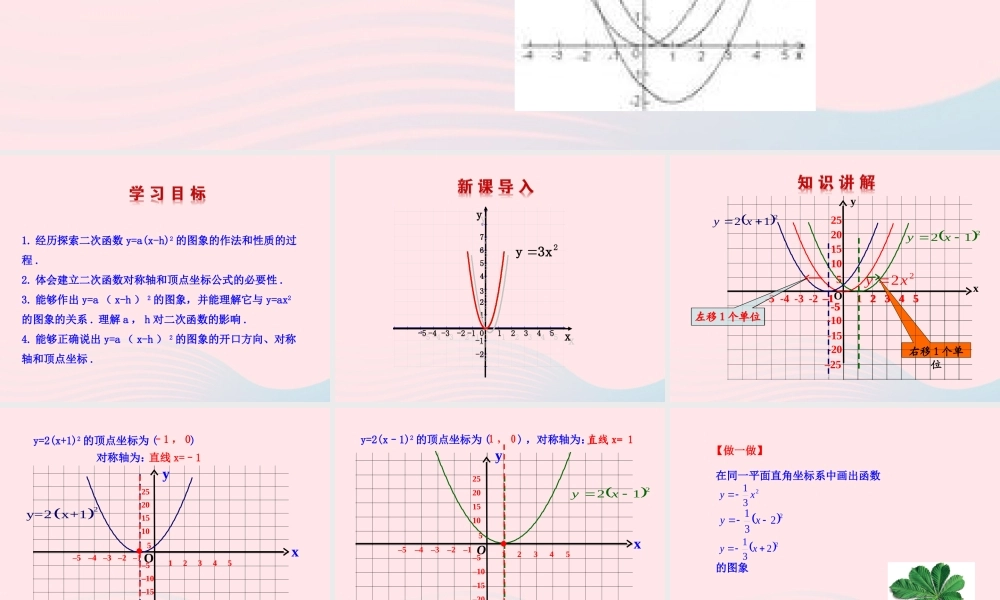
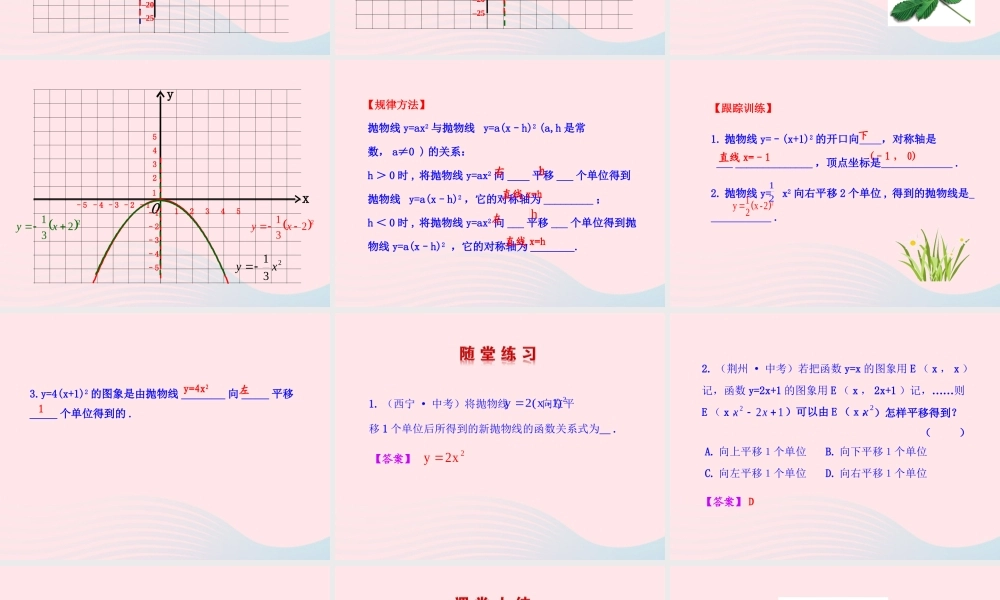
2. 二次函数 y=ax2+bx+c 的图象与性质 ( 第 2 课时 )1. 经历探索二次函数 y=a(x-h)2 的图象的作法和性质的过程 .2. 体会建立二次函数对称轴和顶点坐标公式的必要性 .3. 能够作出 y=a （ x-h ） 2 的图象，并能理解它与 y=ax2的图象的关系 . 理解 a ， h 对二次函数的影响 .4. 能够正确说出 y=a （ x-h ） 2 的图象的开口方向、对称轴和顶点坐标 .8642-2-4-6-10-5510xxyy111122223333444455556677-1-1-1-1-2-2-3-3-4-4-5-500-2-223xy 22xy xy–1 –1 O1 2 34 5510152025-5 -4 -3 -2 –25 -20 -15 -5 212xy212xy右移 1 个单位左移 1 个单位2 34 5-10 -5 左移 1 个单位–1 Oxy12345510152025–5 –4 –3 –2 –25 –20 –15–10 –5 2y=2 x+1y=2(x+1)2 的顶点坐标为 ( ) 对称轴为：–1 ， 0 直线 x=–1Oxy12345510152025–5 –4 –3 –2 –1 –25–20–15–10 –5 212xyy=2(x–1)2 的顶点坐标为 ( ) ，对称轴为：1 ， 0直线 x= 1在同一平面直角坐标系中画出函数的图象231 xy2231xy2231xy【做一做】Ox1234512345–5 –4 –3 –2 –1 –5 –4 –3 –2 –1 y231 xy2231xy2231xy抛物线 y=ax2 与抛物线 y=a(x–h)2 (a,h 是常数， a≠0 ) 的关系：h ＞ 0 时 , 将抛物线 y=ax2 向 ____ 平移 ___ 个单位得到抛物线 y=a(x–h)2 ，它的对称轴为 _________ ；h ＜ 0 时 , 将抛物线 y=ax2 向 ___ 平移 ___ 个单位得到抛物线 y=a(x–h)2 ，它的对称轴为 ________.右h直线 x=h左直线 x=hh【规律方法】1. 抛物线 y=–(x+1)2 的开口向 ，对称轴是 ______________ ，顶点坐标是 .2. 抛物线 y= x2 向右平移 2 个单位 , 得到的抛物线是 .下直线 x=–1 (–1 ， 0)21yx-2212【跟踪训练】3.y=4(x+1)2 的图象是由抛物线 ________ 向 _____ 平移_____ 个单位得到的 .左1y=4x2移 1 个单位后所得到的新抛物线的函数关系式为 .1. （西宁 · 中考）将抛物线向左平2y2(x -1)2x2y 【答案】2. （荆州 · 中考）若把函数 y=x 的图象用 E （ x ， x ）记，函数 y=2x+1 的图象用 E （ x ， 2x+1 ）记，……则E （ x ，）可以由 E （ x ，）怎样平移得到？ （ ）122xx2xA. 向上平移１个单位B. 向下平移１个单位C. 向左平移１个单位D. 向右平移１个单位【答案】 D3. 函数 y=–5(x–3)2, 当 x_____ 时 ,y 随 x 的增大而增大 .4. 对于函数 y=2x2+8x+8 ，当 x=______ 时，函数值 y 有最_____ 值，最小值为 ______.＜ 3–2小0y=a(x–h)2(a,h 是常数， a≠0 ) 的图象和性质y=a(x–h)2开口方向对称轴顶点坐标 a ＞ 0 a ＜ 0向上直线 x=h(h ， 0)向下直线 x=h(h ， 0)忍耐和时间往往比力量和愤怒更有效 . —— 拉封丹