人教版高一数学正弦函数 余弦函数的图象和性质 课件VIP免费

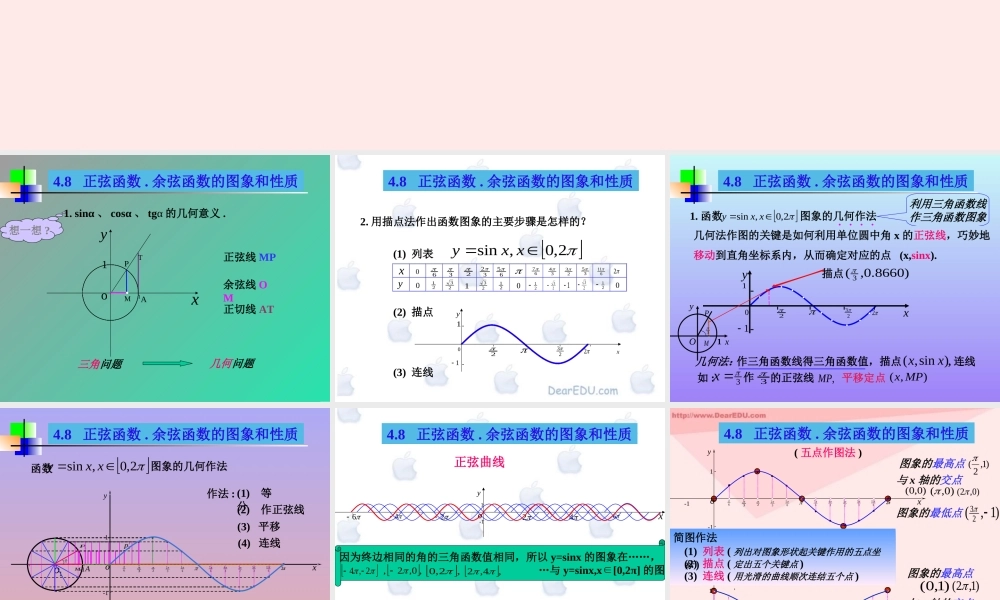
正弦函数 余弦函数的图象和性质 1. sinα 、 cosα 、 tgα 的几何意义 . oxy11PMAT正弦线 MP余弦线 OM正切线 AT想一想 ?三角问题几何问题4.8 正弦函数 . 余弦函数的图象和性质(1) 列表(2) 描点(3) 连线632326567342335611202123012123212300212312,0,sinxxy2. 用描点法作出函数图象的主要步骤是怎样的？---223xy0211---xy4.8 正弦函数 . 余弦函数的图象和性质 1. 函数2,0,sinxxy图象的几何作法. . . .利用三角函数线作三角函数图象223xy11-----02-描点法 : 查三角函数表得三角函数值 , 描点 , 连线 .)sin,(xx查表8660.0sin 3 y如 :3x描点)8660.0,( 3几何法：作三角函数线得三角函数值，描点)sin,(xx, 连线作如 :3x3 的正弦线,MP平移定点),(MPxPM31Oxy几何法作图的关键是如何利用单位圆中角 x 的正弦线，巧妙地移动到直角坐标系内，从而确定对应的点 (x,sinx).4.8 正弦函数 . 余弦函数的图象和性质 2 函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法 : (1) 等分3232656734233561126(2) 作正弦线(3) 平移61P1M/1p(4) 连线4.8 正弦函数 . 余弦函数的图象和性质4.8 正弦函数 . 余弦函数的图象和性质因为终边相同的角的三角函数值相同，所以 y=sinx 的图象在……， …与 y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2正弦曲线xy---------1-12o46246余弦曲线（平移得到）余弦曲线（几何作法）4.8 正弦函数 . 余弦函数的图象和性质与 x 轴的交点)0,0()0,()0,2( 图象的最高点图象的最低点)1,( 23 与 x 轴的交点)0,( 2)0,( 23图象的最高点)1,0()1,2( 图象的最低点)1,(( 五点作图法 )2oxy---11--13232656734233561126-oxy---11--13232656734233561126)1,2(简图作法(1) 列表 ( 列出对图象形状起关键作用的五点坐标 )(3) 连线 ( 用光滑的曲线顺次连结五个点 )(2) 描点 ( 定出五个关键点 ) 4.8 正弦函数 . 余弦函数的图象和性质例 1 ．画出下列函数的简图（ 1 ） y=sinx+1, x∈[0,2π]列表描点作图-2223211-xyo-xxsin1sinx101010210102232（ 2 ）...