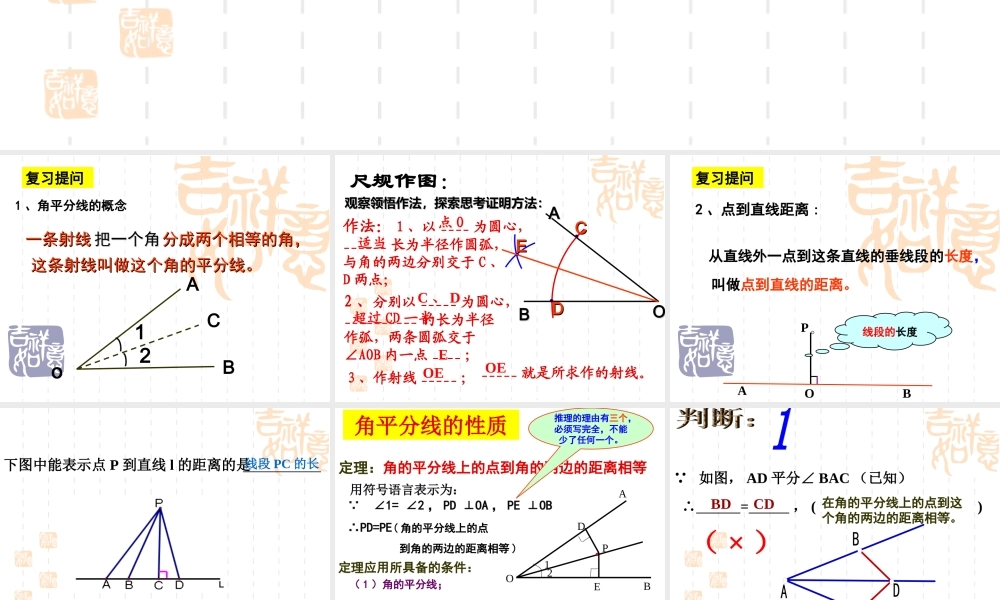
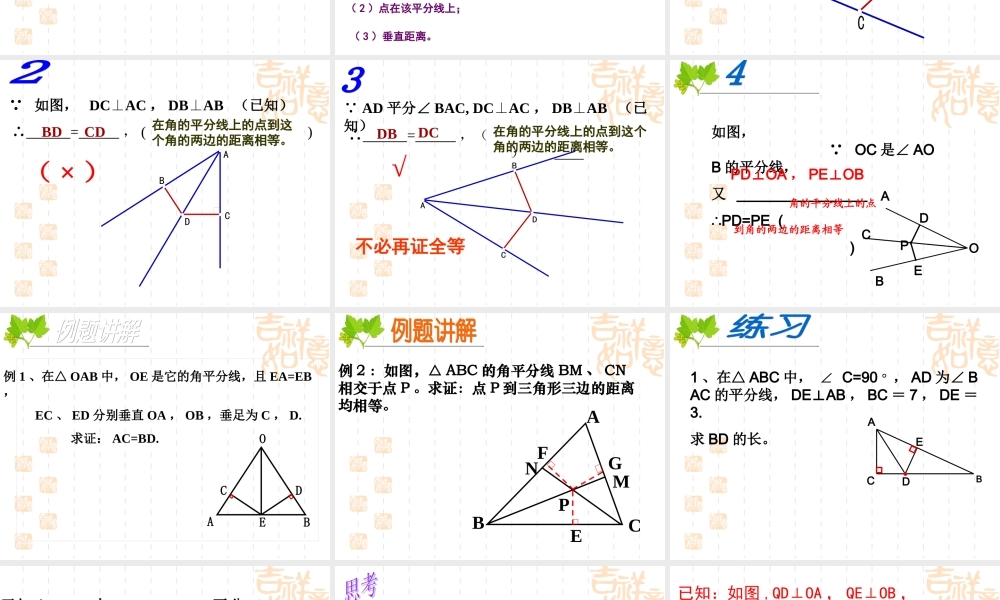
13.5.2 角平分线 复习提问1 、角平分线的概念一条射线一条射线 把一个角把一个角分成两个相等的角,分成两个相等的角,这条射线叫做这个角的平分线。这条射线叫做这个角的平分线。oBCA12 AAOOBBCCDDEE尺规作图:作法: 1 、以 ____ 为圆心,______ 长为半径作圆弧,与角的两边分别交于 C 、D 两点;2 、分别以 _____ 为圆心,__________ 的长为半径作弧,两条圆弧交于∠AOB 内一点 ____ ;3 、作射线 _____ ; _____ 就是所求作的射线。点 O适当C 、 D超过 CD 一半EOEOE观察领悟作法,探索思考证明方法:观察领悟作法,探索思考证明方法: 复习提问 2 、点到直线距离 :从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。OPAB线段的长度 下图中能表示点 P 到直线 l 的距离的是线段 PC 的长角平分线的性质定理:角的平分线上的点到角的两边的距离相等用符号语言表示为:AOBPED12 ∠1= ∠2 , PD ⊥OA , PE ⊥OB∴PD=PE( 角的平分线上的点 到角的两边的距离相等 )推理的理由有三个,必须写完全,不能少了任何一个。定理应用所具备的条件: ( 1 )角的平分线;( 2 )点在该平分线上; ( 3 )垂直距离。 如图, AD 平分∠ BAC (已知) ∴ = , ( ) 在角的平分线上的点到这个角的两边的距离相等。ADCBBD CD( × ) 如图, DCAC⊥, DBAB ⊥(已知) ∴ = , ( ) 在角的平分线上的点到这个角的两边的距离相等。ADCBBD CD( × ) AD 平分∠ BAC, DCAC⊥, DBAB ⊥(已知)∴ = ,( ) DBDC在角的平分线上的点到这个角的两边的距离相等。ADCB√不必再证全等 如图, OC 是∠ AOB 的平分线, 又 ________________∴PD=PE ( )PDOA⊥, PEOB⊥BOACDPE 角的平分线上的点 到角的两边的距离相等 例 1 、在△ OAB 中, OE 是它的角平分线,且 EA=EB, EC 、 ED 分别垂直 OA , OB ,垂足为 C , D. 求证: AC=BD.OABECD 例 2 :如图,△ ABC 的角平分线 BM 、 CN相交于点 P 。求证:点 P 到三角形三边的距离均相等。ABCPEFGMN 1 、在△ ABC 中, ∠ C=90 ° , AD 为∠ BAC 的平分线, DEAB⊥, BC = 7 , DE =3.求 BD 的长。EDCBA 2 、已知△ ABC 中 , C=90∠0,AD 平分∠ CAB,且 BC=8,BD=5, 求点 D 到 AB 的距离是 ABCDE 反过来...