人教版高一数学正弦、余弦函数的定义域、值域课件VIP免费

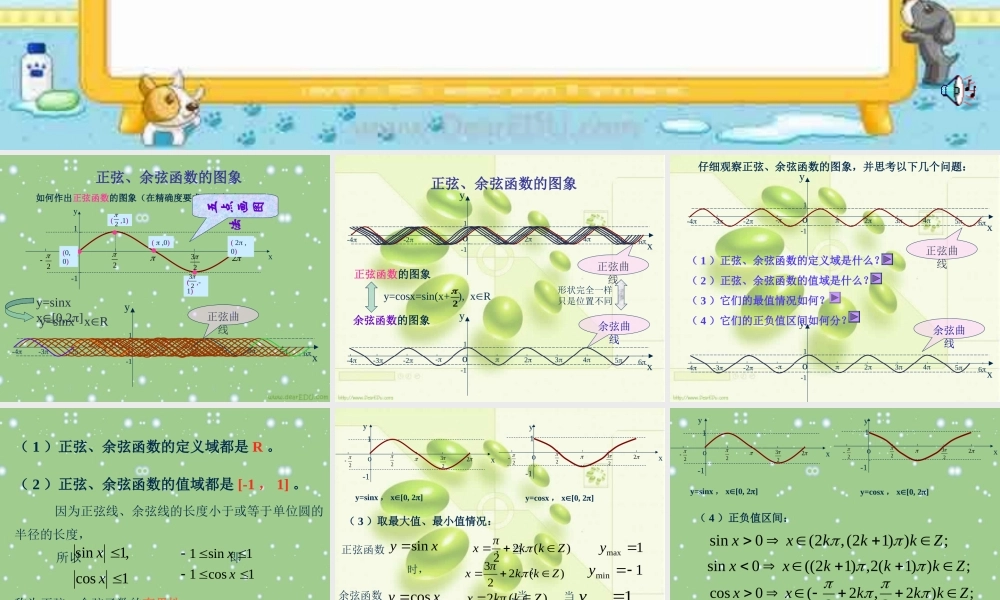
正弦、余弦函数的定义域、值域 正弦、余弦函数的图象 x6yo--12345-2-3-41y=sinx x[0,2]y=sinx xR正弦曲线yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)五点画图法x6yo--12345-2-3-41 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 x6yo--12345-2-3-41y=cosx=sin(x+ ), xR2余弦曲线正弦曲线形状完全一样只是位置不同x6yo--12345-2-3-41x6yo--12345-2-3-41仔细观察正弦、余弦函数的图象，并思考以下几个问题：（ 1 ）正弦、余弦函数的定义域是什么？（ 2 ）正弦、余弦函数的值域是什么？（ 3 ）它们的最值情况如何？（ 4 ）它们的正负值区间如何分？正弦曲线余弦曲线（ 1 ）正弦、余弦函数的定义域都是 R 。（ 2 ）正弦、余弦函数的值域都是 [-1 ， 1] 。 因为正弦线、余弦线的长度小于或等于单位圆的半径的长度， 所以 即称为正弦、余弦函数的有界性。1cos,1sinxx1cos11sin1xx余弦函数 , 当 时， ； 当 时， xycos)(2Zkkπx1max y).()12(Zkπkx1miny-1yxo122322y=cosx ， x[0, 2]yxo1-122322y=sinx ， x[0, 2]正弦函数 ， 当 时， ; 当 时， ；xysin)(22Zkkπx1max y)(223Zkkπx1miny（ 3 ）取最大值、最小值情况：（ 4 ）正负值区间： ;))12(,2(0sinZkkkxx;))1(2,)12((0sinZkkkxx;)22,22(0cosZkkkxx.)223,22(0cosZkkkxx-1yxo122322y=cosx ， x[0, 2]yxo1-122322y=sinx ， x[0, 2] 例 1 求下列函数的定义域：xycos)1(xysin3)2(xycoslg)3(xysin11)4(解：}{Rxx解：要使 有意义，只须 即 解之得xysin30sin3x0sinx},)1(2)12({Zkπkxπkx解：要使 有意义，只须 解之得xycoslg0cosx};,2222{Zkkxkx解：由 得即,0sin1x1sinx},223{Zkkππxx解：使函数 取得最大值的 x 的集合，就是使函数 取得最大值的 x 的集合 Rxxy,1cosRxxy,cos},2{πkkπxxRxxy,1cos函数...