名师讲解1 九年级数学下实际问题与二次函数课件人教版VIP免费

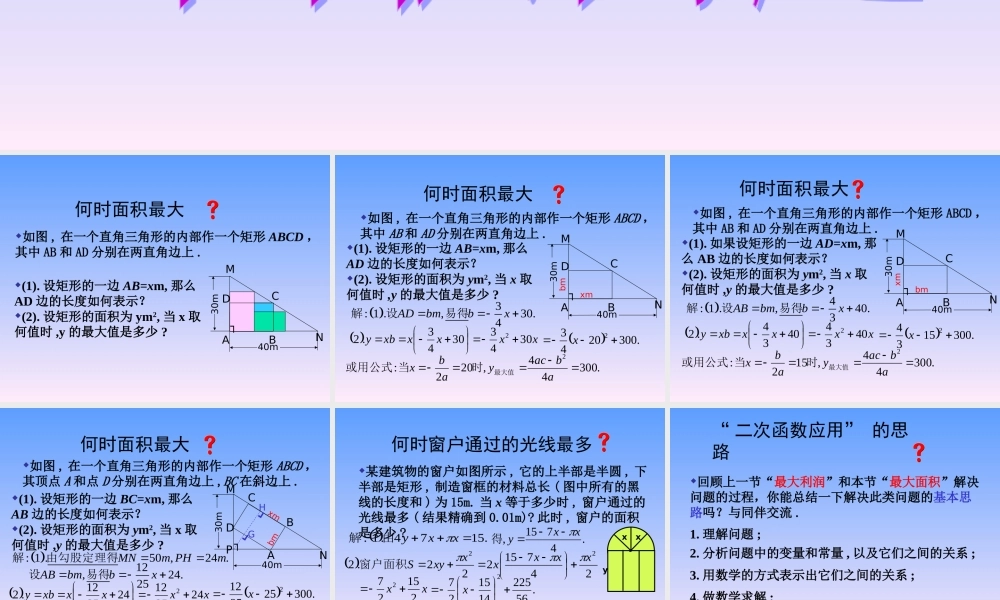
(1). 设矩形的一边 AB=xm, 那么AD 边的长度如何表示？(2). 设矩形的面积为 ym2, 当 x 取何值时 ,y 的最大值是多少 ?何时面积最大 如图 , 在一个直角三角形的内部作一个矩形 ABCD ，其中 AB 和 AD 分别在两直角边上 .MN40m30mABCD┐(1). 设矩形的一边 AB=xm, 那么AD 边的长度如何表示？(2). 设矩形的面积为 ym2, 当 x 取何值时 ,y 的最大值是多少 ?何时面积最大 如图 , 在一个直角三角形的内部作一个矩形 ABCD ，其中 AB 和 AD 分别在两直角边上 .ABCD┐MN 3: 1 .,30.4ADbmbx解设易得40m30m xxxxxby30433043.22 .30020432 x.30044,202:2abacyabx最大值时当或用公式xmbm(1). 如果设矩形的一边 AD=xm, 那么 AB 边的长度如何表示？(2). 设矩形的面积为 ym2, 当 x 取何值时 ,y 的最大值是多少 ?何时面积最大 如图 , 在一个直角三角形的内部作一个矩形 ABCD ，其中 AB 和 AD 分别在两直角边上 .ABCD┐MN40m30mbmxm 4: 1 .,40.3ABbmbx解设易得 xxxxxby40344034.22 .30015342 x.30044,152:2abacyabx最大值时当或用公式(1). 设矩形的一边 BC=xm, 那么AB 边的长度如何表示？(2). 设矩形的面积为 ym2, 当 x 取何值时 ,y 的最大值是多少 ?何时面积最大 如图 , 在一个直角三角形的内部作一个矩形 ABCD ，其顶点 A 和点 D 分别在两直角边上 ,BC 在斜边上 .ABCD┐MNP40m30mxmbm : 1 .50 ,24 .MNm PHm解由勾股定理得 xxxxxby242512242512.22 .3002525122 x.30044,252:2abacyabx最大值时当或用公式12,24.25ABbmbx设易得HG┛┛何时窗户通过的光线最多某建筑物的窗户如图所示 , 它的上半部是半圆 , 下半部是矩形 , 制造窗框的材料总长 ( 图中所有的黑线的长度和 ) 为 15m. 当 x 等于多少时 , 窗户通过的光线最多 ( 结果精确到 0.01m)? 此时 , 窗户的面积是多少 ?xxy .1574.1:xxy由解.4715,xxy得xx215272  24715222.222xxxxxxyS窗户面积.02.45622544,07.114152:2abacyabx最大值时当或用公式.562251415272x1. 理解问题 ;“ 二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程，你能总结一下解决此类问题的基本思路吗？与同伴交流 .2. 分析问题中的变量和常量 , 以及它们之间的关系 ;3. 用数学的方式表示出它们之间的关系 ;4. 做数学求解 ;5. 检验结果的合理性 , 拓展等 .