山西省忻州市高考数学 专题 圆圆位置关系复习课件VIP免费

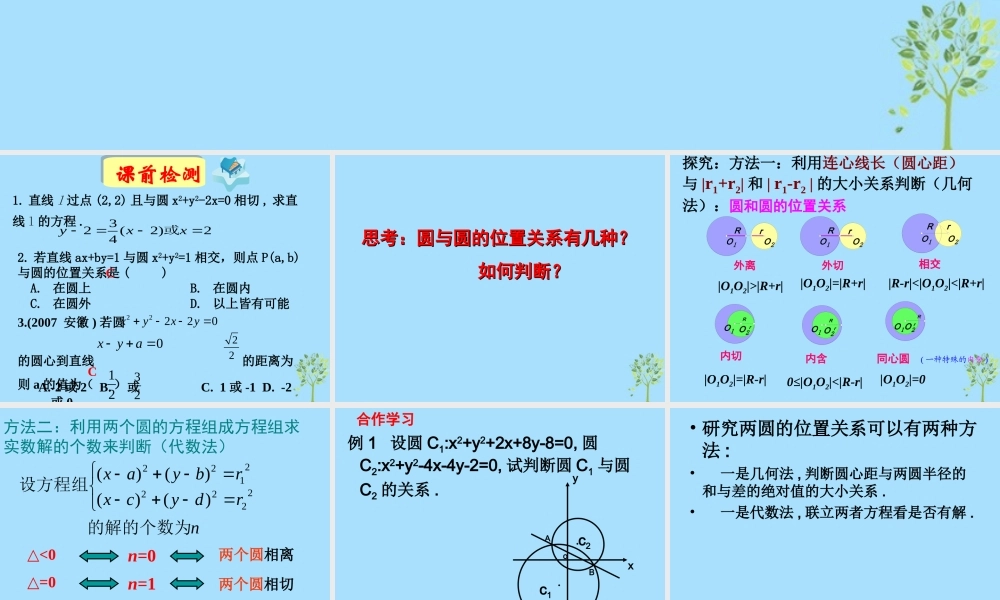
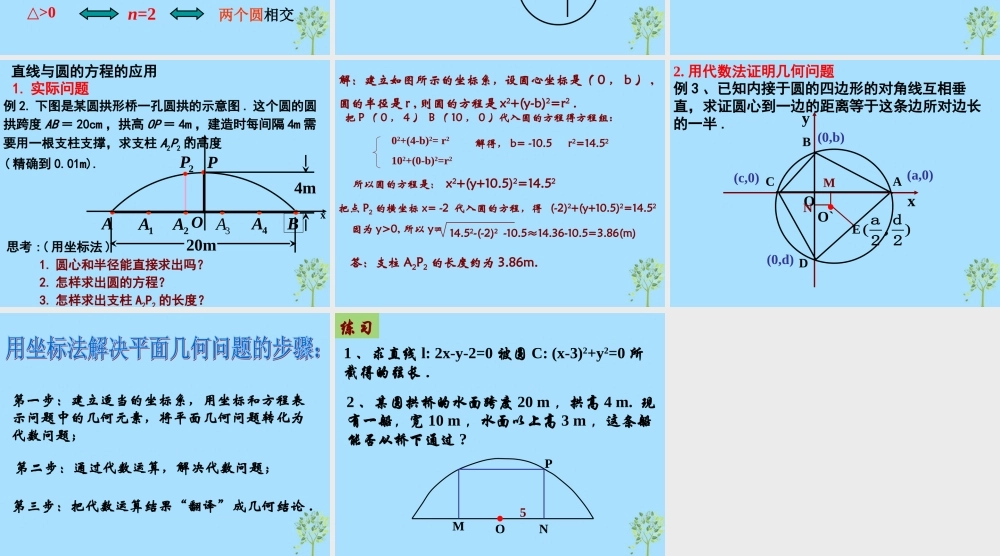
圆圆位置关系课前检测2. 若直线 ax+by=1 与圆 x2+y2=1 相交，则点 P(a,b)与圆的位置关系是 ( ) A. 在圆上 B. 在圆内 C. 在圆外 D. 以上皆有可能 C3.(2007 安徽 ) 若圆 的圆心到直线 的距离为则 a 的值为（ ）22220xyxy0xya22CA.-2 或 2 B. 或 C. 1 或 -1 D. -2或 032121. 直线 l 过点 (2,2) 且与圆 x2+y2-2x=0 相切 , 求直线 l 的方程 . 2)2(432xxy或思考：圆与圆的位置关系有几种？思考：圆与圆的位置关系有几种？ 如何判断？如何判断？外离|O1O2|>|R+r||O1O2|=|R+r||R-r|<|O1O2|<|R+r||O1O2|=|R-r|0≤|O1O2|<|R-r||O1O2|=0外切相交内切内含同心圆( 一种特殊的内含 )rRO1O2rRO1O2rRO1O2rRO1 O2rRO1 O2rRO1O2探究：方法一：利用连心线长（圆心距）与 |r1+r2| 和 | r1-r2 | 的大小关系判断（几何法）：圆和圆的位置关系方法二：利用两个圆的方程组成方程组求实数解的个数来判断（代数法）nrdycxrbyax的解的个数为设方程组 )()()()(22222122n=0两个圆相离△<0n=1两个圆相切△=0n=2两个圆相交△>0例 1 设圆 C1:x2+y2+2x+8y-8=0, 圆C2:x2+y2-4x-4y-2=0, 试判断圆 C1 与圆C2 的关系 . yxABoc1c2合作学习• 研究两圆的位置关系可以有两种方法 :• 一是几何法 , 判断圆心距与两圆半径的和与差的绝对值的大小关系 .• 一是代数法 , 联立两者方程看是否有解 .例 2. 下图是某圆拱形桥一孔圆拱的示意图 . 这个圆的圆拱跨度 AB ＝ 20cm ，拱高 OP ＝ 4m ，建造时每间隔 4m 需要用一根支柱支撑，求支柱 A2P2 的高度( 精确到 0.01m).1. 实际问题直线与圆的方程的应用A1A2A3A4AB2PPO4m20myx思考 :( 用坐标法 )1. 圆心和半径能直接求出吗？2. 怎样求出圆的方程？3. 怎样求出支柱 A2P2 的长度？解：建立如图所示的坐标系，设圆心坐标是（ 0 ， b ） ,圆的半径是 r , 则圆的方程是 x2+(y-b)2=r2 .把 P （ 0 ， 4 ） B （ 10 ， 0 ）代入圆的方程得方程组：02+(4-b)2= r2102+(0-b)2=r2解得， b= -10.5 r2=14.52所以圆的方程是： x2+(y+10.5)2=14.52把点 P2 的横坐标 x= -2 代入圆的方程，得 (-2)2+(y+10.5)2=14.52因为 y>0, 所以 y= 14.52-(-2)2 -10.5≈14.36-10.5=3.86(m)答：支柱 A2P2 的长度约为 3.86m.E例 3 、已知内接于圆的四边形的对角线互相垂 直，...