九年级数学下册 34弧长和扇形的面积，圆锥的侧面展开图-341弧长和扇形的面积(2)课件 湘教版 课件VIP免费

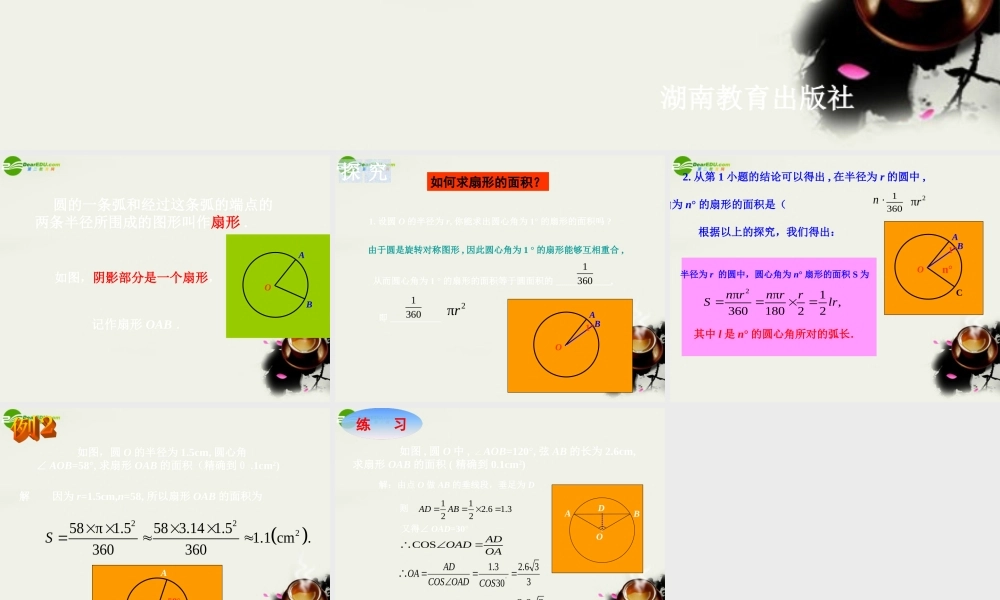
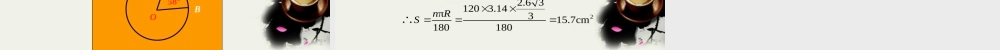义务教育课程标准实验教科书SHUXUE 九年级下湖南教育出版社 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形 .记作扇形 OAB ．如图，阴影部分是一个扇形，OAB·即 ___________探 究2πr如何求扇形的面积？1. 设圆 O 的半径为 r, 你能求出圆心角为 1° 的扇形的面积吗 ?由于圆是旋转对称图形 , 因此圆心角为 1 ° 的扇形能够互相重合 ,从而圆心角为 1 ° 的扇形的面积等于圆面积的 ____________,13601360OAB·1°根据以上的探究，我们得出：2ππ1,36018022n rn rrSlr其中 l 是 n° 的圆心角所对的弧长．半径为 r 的圆中，圆心角为 n° 扇形的面积 S 为2. 从第 1 小题的结论可以得出 , 在半径为 r 的圆中 ,圆心角为 n° 的扇形的面积是（ ） n2πr1360OAB·1°Cn° 如图，圆 O 的半径为 1.5cm, 圆心角∠ AOB=58°, 求扇形 OAB 的面积（精确到０ .1cm2) 解 因为 r=1.5cm,n=58, 所以扇形 OAB 的面积为22258 π 1.558 3.14 1.51.1 cm.360360S OAB·58° 如图 , 圆 O 中 , ∠AOB=120°, 弦 AB 的长为 2.6cm,求扇形 OAB 的面积 ( 精确到 0.1cm2)·OBA练 习解：由点 O 做 AB 的垂线段，垂足为 D则112.61.322ADAB 又得∠ OAD=30°1.32.6 3330ADOACOS OADCOS22.6 31203.14π315.7cm180180n RSCOSADOADOAD