九年级数学下册 第27章二次函数272二次函数的图象与性质 2二次函数yax2bxc的图象与性质(第1课时)课件 华东师大版 课件VIP免费

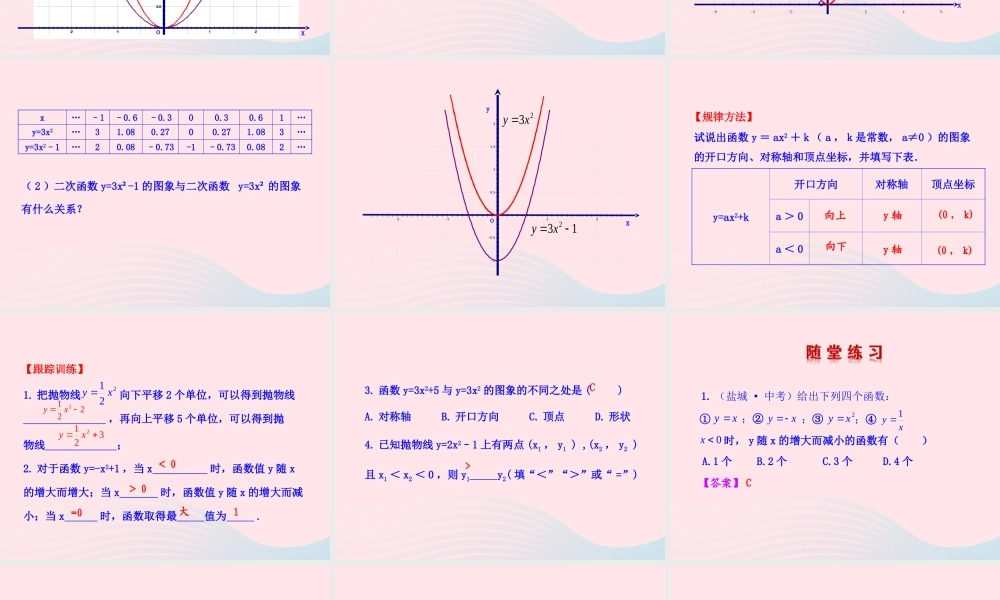
2. 二次函数 y=ax2+bx+c 的图象与性质 ( 第 1 课时 )的图象，并能够比较它与二次函数2yaxc2yax1. 能作出二次函数与ac对二次函数图象的影响 .的图象的异同，理解和2yax2yaxc2. 能说出二次函数图象的开口方向、对称轴和顶点坐标 .2xy 2xy比较二次函数 y=x² 和 y=–x² 图象的异同：4321-1-2-3-4-5-6-4-2246 y x o二次函数 y=2x² 的图象是什么形状？它与二次函数y=x² 的图象有什么相同和不同？2xy 22xy  y x ox…–1.5–1–0.500.511.5…y=2x2…4.520.500.524.5…y=2x2+1…5.531.511.535.5…（ 1 ）二次函数 y=2x² ＋ 1 的图象与二次函数 y=2x² 的图象有什么关系？ o122  xy22xy  y x7654321-6-4-2246（ 2 ）二次函数 y=3x²-1 的图象与二次函数 y=3x² 的图象有什么关系？x…–1–0.6–0.300.30.61…y=3x2…31.080.2700.271.083…y=3x2–1…20.08–0.73-1–0.730.082… x21.510.5-0.5-1-2-112 y o132  xy23xy 试说出函数 y ＝ ax2 ＋ k （ a ， k 是常数， a≠0 ）的图象的开口方向、对称轴和顶点坐标，并填写下表． 【规律方法】y=ax2+k开口方向对称轴顶点坐标a ＞ 0a ＜ 0向上向下y 轴y 轴(0 ， k)(0 ， k)1. 把抛物线 向下平移 2 个单位，可以得到抛物线 ，再向上平移 5 个单位，可以得到抛物线 ；2. 对于函数 y=-x2+1 ，当 x 时，函数值 y 随 x的增大而增大；当 x 时，函数值 y 随 x 的增大而减小；当 x 时，函数取得最 值为 .221 xy 2212 xy3212 xy＜ 0＞ 0=0大1【跟踪训练】3. 函数 y=3x2+5 与 y=3x2 的图象的不同之处是 ( )A. 对称轴 B. 开口方向 C. 顶点 D. 形状4. 已知抛物线 y=2x2–1 上有两点 (x1 ， y1 ) ,(x2 ， y2 )且 x1 ＜ x2 ＜ 0 ，则 y1 y2( 填“＜”“＞”或“ =”)C>【答案】 C1. （盐城 · 中考）给出下列四个函数：0x；②xyxy xy12xy ；③；④①时， y 随 x 的增大而减小的函数有（ ）A.1 个 B.2 个 C.3 个 D.4 个轴的交点的个数是（ ）A.3 个B.2 个C.1 个D.0 个21yxx2. （济南 · 中考）在平面直角坐标系中，抛物线与【答案】 B3. 直角坐标平面上有一函数 y=24x248 的图象，其顶点坐标是（ ）A.(0 ， 2) B.(1 ， 24) C.(0 ， 48) D.(2 ， 48)【答...