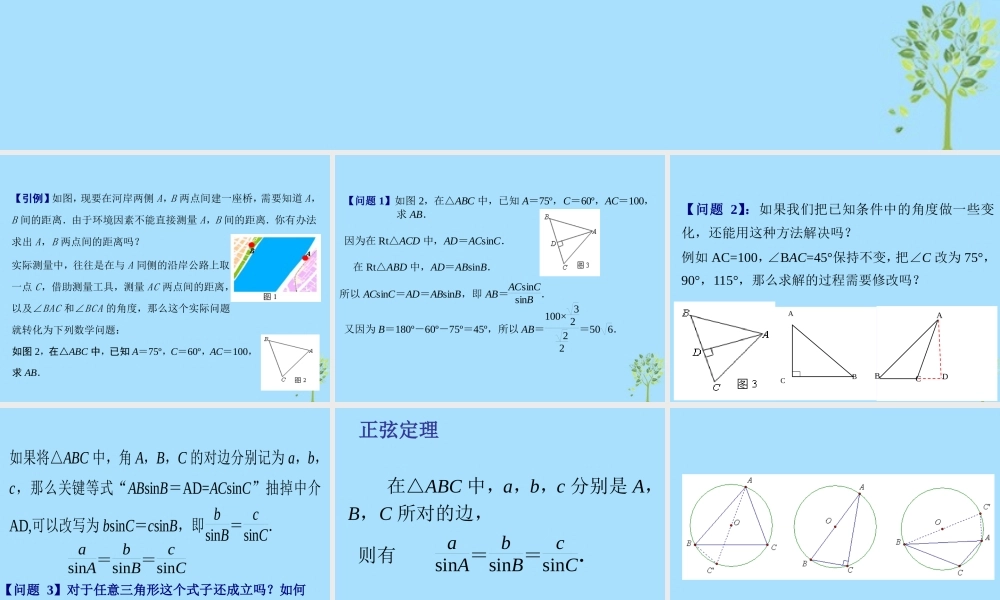
正弦定理(一)【引例】如图,现要在河岸两侧 A,B 两点间建一座桥,需要知道 A,B 间的距离.由于环境因素不能直接测量 A,B 间的距离.你有办法求出 A,B 两点间的距离吗? 实际测量中,往往是在与 A 同侧的沿岸公路上取一点 C,借助测量工具,测量 AC 两点间的距离,以及∠BAC 和∠BCA 的角度,那么这个实际问题就转化为下列数学问题: 如图 2,在△ABC 中,已知 A=75º,C=60º,AC=100,求 AB. 在 Rt△ABD 中,AD=ABsinB. 【问题 1】如图 2,在△ABC 中,已知 A=75º,C=60º,AC=100,求 AB. 因为在 Rt△ACD 中,AD=ACsinC. 所以 ACsinC=AD=ABsinB,即 AB=ACsinCsinB . 又因为 B=180º-60º-75º=45º,所以 AB=100× 3222=50 6. 【问题 2】:如果我们把已知条件中的角度做一些变化,还能用这种方法解决吗? 例如 AC=100,∠BAC=45°保持不变,把∠C 改为 75°,90°,115°,那么求解的过程需要修改吗? CABBACD如果将△ABC 中,角 A,B,C 的对边分别记为 a,b,c,那么关键等式“ABsinB=AD=ACsinC”抽掉中介AD,可以改写为 bsinC=csinB,即 bsinB= csinC. 【问题 3】对于任意三角形这个式子还成立吗?如何验证你的猜想? asinA= bsinB= csinC 在△ABC 中,a,b,c 分别是 A,B,C 所对的边, 则有 asinA= bsinB= csinC. 正弦定理 在△ABC 中,a,b,c 分别是 A,B,C 所对的边,则有 asinA= bsinB= csinC. 正弦定理【问题 4】说说你对正弦定理的认识! 谈谈你的收获! 证明途径 (1) 转化为直角三角形的边角关系; (2) 建立直角坐标系,利用三角函数的定义; (3) 通过三角的形外接圆,将任意三角形问 题转化为直角三角形问题; (4) 利用向量的数量积产生三角函数; …… 感谢指导!