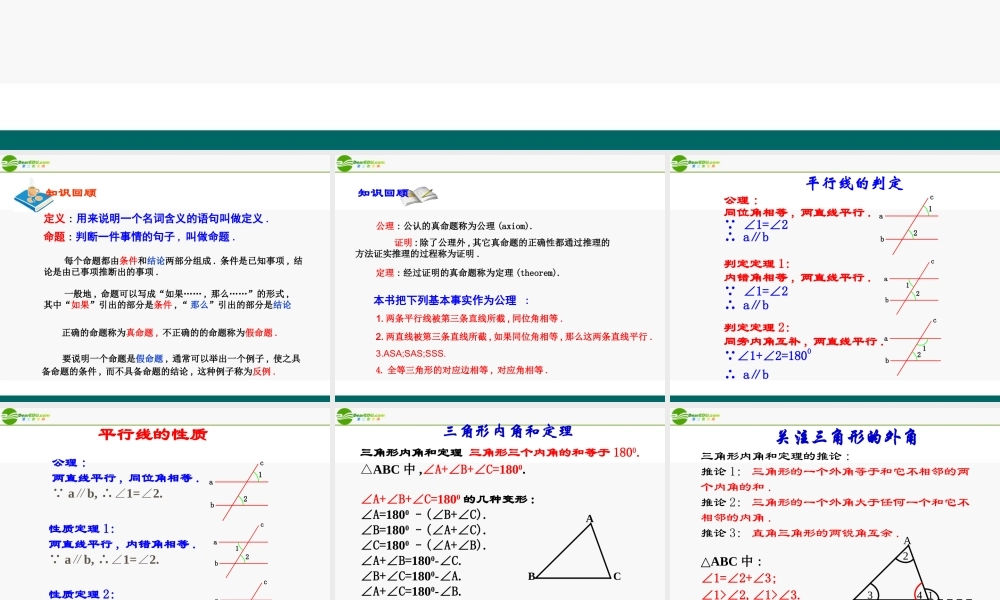
回顾与思考第 11 章 几何证明初步 要说明一个命题是假命题 , 通常可以举出一个例子 , 使之具备命题的条件 , 而不具备命题的结论 , 这种例子称为反例 . 定义 : 用来说明一个名词含义的语句叫做定义 . 命题 : 判断一件事情的句子 , 叫做命题 .知识回顾 每个命题都由条件和结论两部分组成 . 条件是已知事项 , 结论是由已事项推断出的事项 . 一般地 , 命题可以写成“如果…… , 那么……”的形式 ,其中“如果”引出的部分是条件 ,“ 那么”引出的部分是结论 正确的命题称为真命题 , 不正确的的命题称为假命题 .定理 : 经过证明的真命题称为定理 (theorem).4. 全等三角形的对应边相等 , 对应角相等 .知识回顾公理 : 公认的真命题称为公理 (axiom). 证明 : 除了公理外 , 其它真命题的正确性都通过推理的方法证实推理的过程称为证明 .本书把下列基本事实作为公理 :1. 两条平行线被第三条直线所截 , 同位角相等 .2. 两直线被第三条直线所截 , 如果同位角相等 , 那么这两条直线平行 .3.ASA;SAS;SSS. 平行线的判定公理 :同位角相等 , 两直线平行 . ∠1=∠2 ∴ a∥b判定定理 1:内错角相等 , 两直线平行 . ∠1=∠2∴ a∥b判定定理 2:同旁内角互补 , 两直线平行 . ∠1+∠2=1800 ∴ a∥b abc12abc12abc12公理 :两直线平行 , 同位角相等 . ab, 1=2.∥∴∠∠性质定理 1:两直线平行 , 内错角相等 . ab, 1=2.∥∴∠∠性质定理 2:两直线平行 , 同旁内角互补 . ab, 1+2=180∥∴ ∠∠0 . 平行线的性质abc12abc12abc12三角形内角和定理三角形内角和定理 三角形三个内角的和等于 1800.△ABC 中 ,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800 的几种变形 :∠A=1800 –(∠B+∠C).∠B=1800 –(∠A+∠C).∠C=1800 –(∠A+∠B).∠A+∠B=1800-∠C.∠B+∠C=1800-∠A.∠A+∠C=1800-∠B.这里的结论 , 以后可以直接运用 . ABC关注三角形的外角三角形内角和定理的推论 :推论 1: 三角形的一个外角等于和它不相邻的两个内角的和 .推论 2: 三角形的一个外角大于任何一个和它不相邻的内角 .推论 3: 直角三角形的两锐角互余 .△ABC 中 : ∠1=∠2+∠3;∠1>∠2,∠1>∠3.ABCD1234这个结论以后可以直接运用 .证明一个命题的一般步骤 :知识回顾( 1 )根据题意,画出图形。( 2 )结合图形,写出已知、求证。( 3 )找出由已知推出...