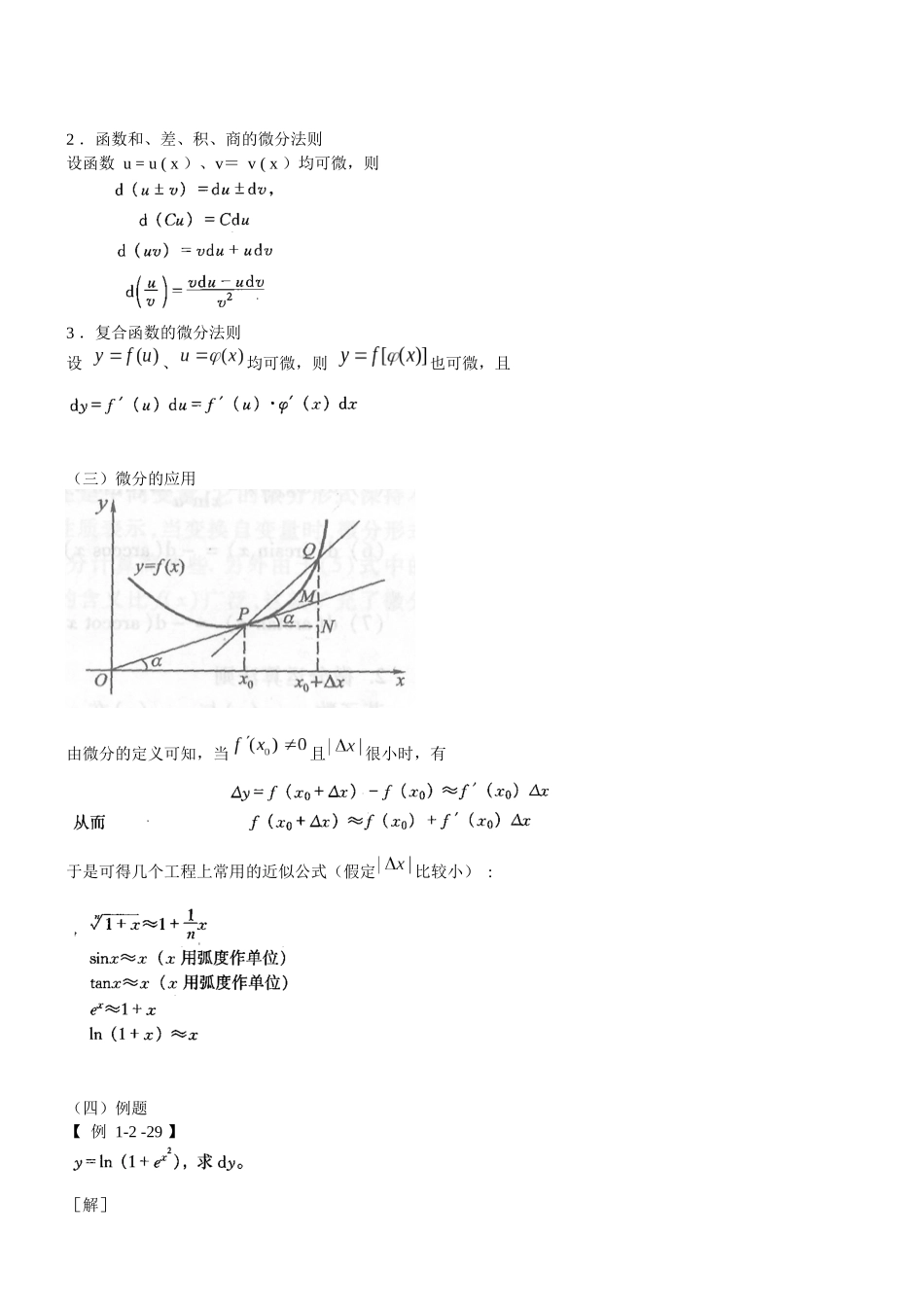
四、微分及其应用(一)微分概念 1 .微分的定义设函数 y = f ( x )在某区间 I 内有定义,。若函数的增量其中 A 是不依赖的常数,则称 y = f ( x )在点 x0可微分,叫做 y = f ( x )在点 x0相应于自变量增量的微分,记作 dy ,即函数 y = f(x)劝在点 x 的微分称为函数 y = f ( x )的微分,记作 dy 或 df ( x)。2 .函数可微分的充分必要条件函数 y = f(x)在点 x0 可微分的充分必要条件是 f ( x )在点 x0 可导,且当 f ( x ) 在点 xo可导时,其微分一定是函数的微分是通常把称为自变量的微分,记作 dx ,即于是函数的微分可写成而导数可写成即导数等于函数的微分 dy 与自变量的微分 dx 之商。(二)基本微分公式与微分法则1 .基本微分公式2 .函数和、差、积、商的微分法则设函数 u = u ( x )、v= v ( x )均可微,则3 .复合函数的微分法则设 、均可微,则 也可微,且(三)微分的应用由微分的定义可知,当且很小时,有于是可得几个工程上常用的近似公式(假定比较小) :(四)例题 【 例 1-2 -29 】[解]【 例 1-2-30 】[解]【 例 1-2 -31 】计算 sin30°30`的近似值。 【解 】 把 sin30°30`化为弧度,得【 例 1-2 - 32 】 计算 的近似值。五、中值定理与导数的应用(一)中值定理 1 .若函数 f ( x )在闭区间[ a ,b]上连续,在开区间( a , b )内可导,且 f ( a ) = f ( b ) ,则至少有一点ξ∈( a, b ) ,使得 f ' (ξ)= 0。2 .拉格朗日中值定理若函数 f ( x )在闭区间[ a ,b]上连续,在开区间( a , b )内可导,则至少有一 点 ξ∈( a, b ),使得下式成立(二)求未定式的值的方法 ― 罗必塔法则1 .未定式与的情形关于要的情形:设( 1 )当 x → a (或 x→∞)时, f (x)→0 且 F ( x ) → 0 ,( 2 ) 在点 a 的某去心邻域内(或当|X|> N 时) , f ' ( x )及 F ' ( x )都存在且 F ' (x)0 ,则 若 仍属型 ,且 f ' ( x )、 F ' (x)满足上述三个条件,则可继续运用罗必塔法则,即对于型,也有相应的罗必塔法则,这里不再赘述。2 .其他形式的未定式的情形其他尚有 0 · 、-、 00 、 1、0 型的未定式,它们均可通过变形化成或的情形。如 0 ·型可变形成或,-型通过通分,...