运筹学课后习题答案VIP免费

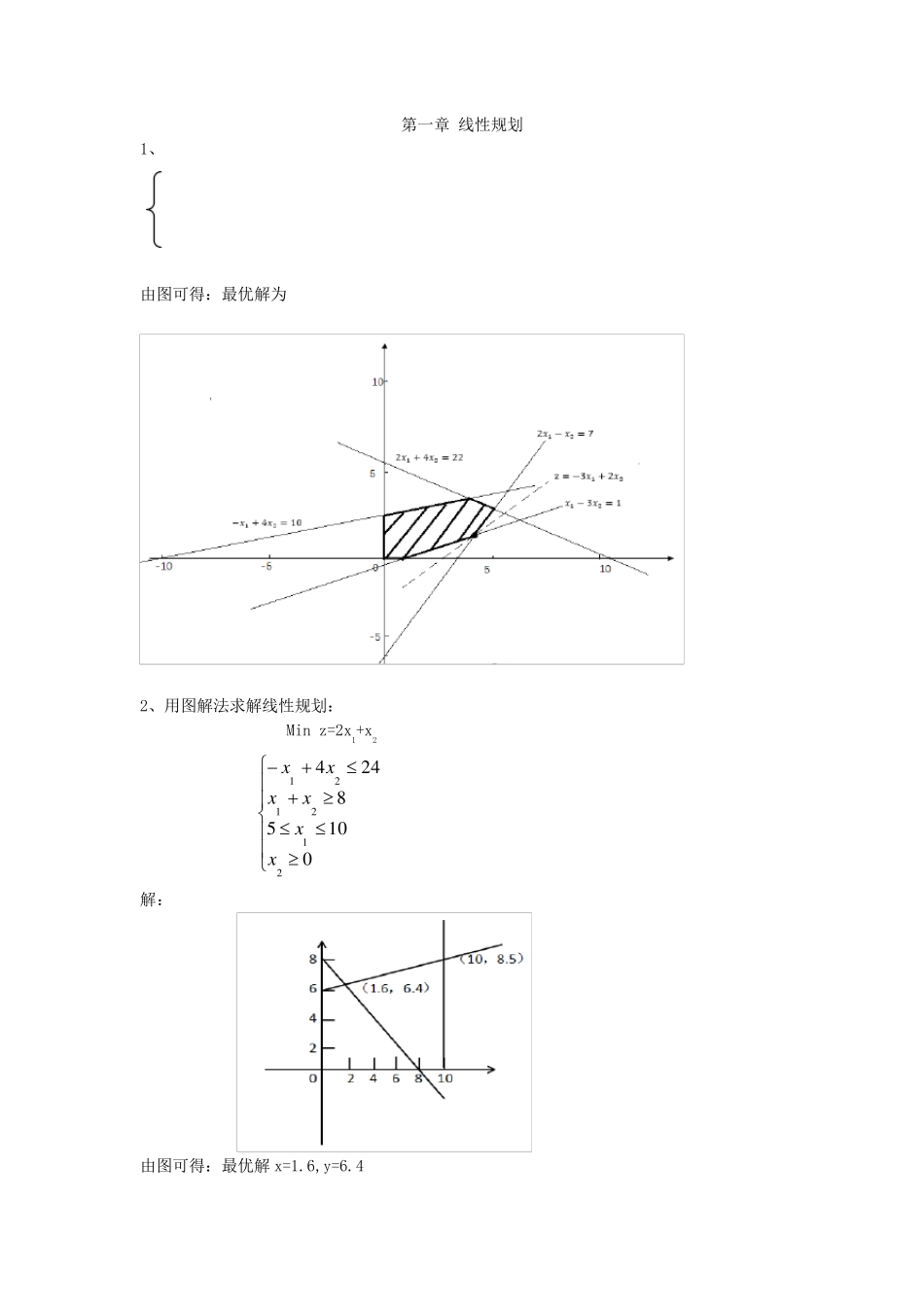
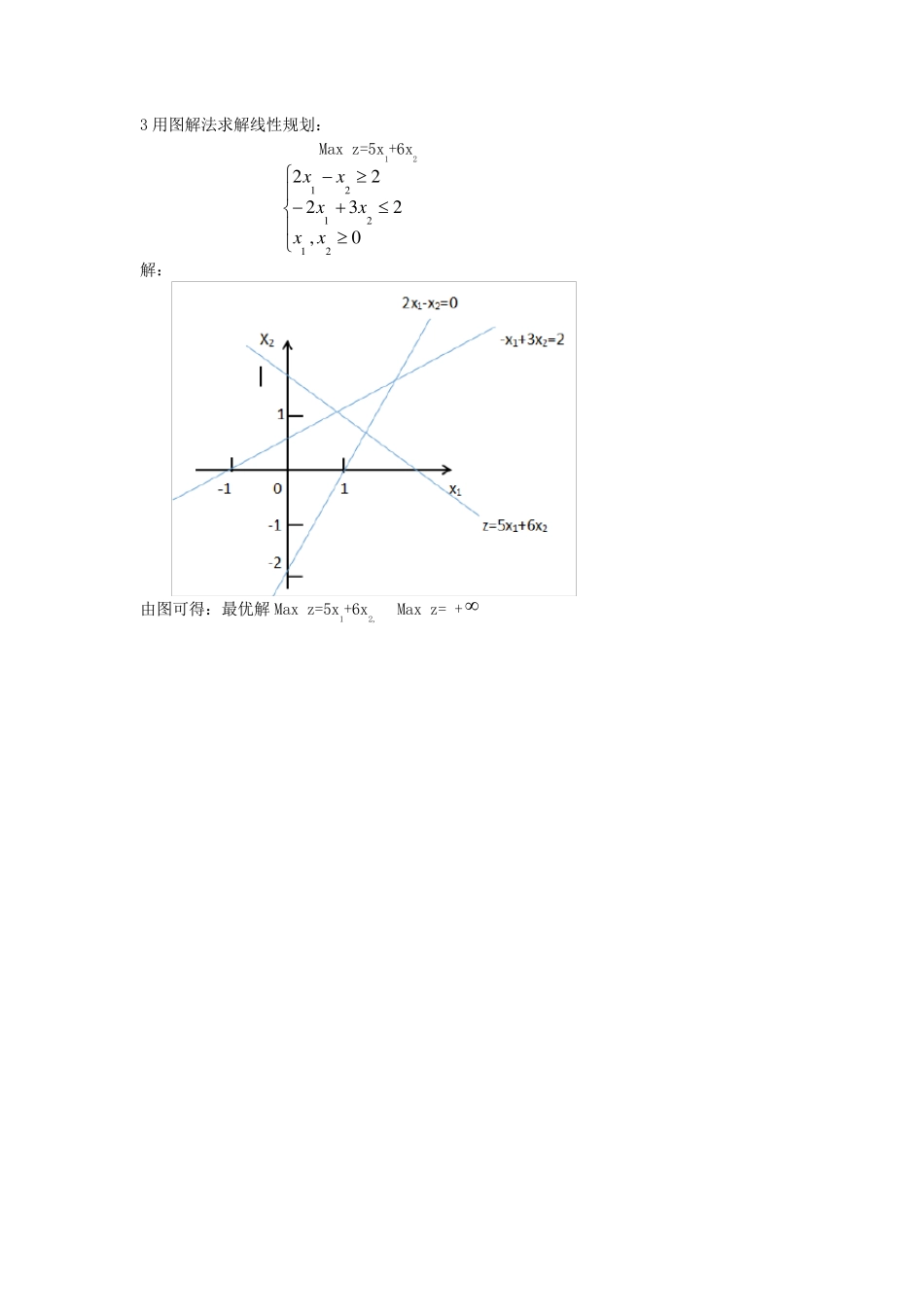
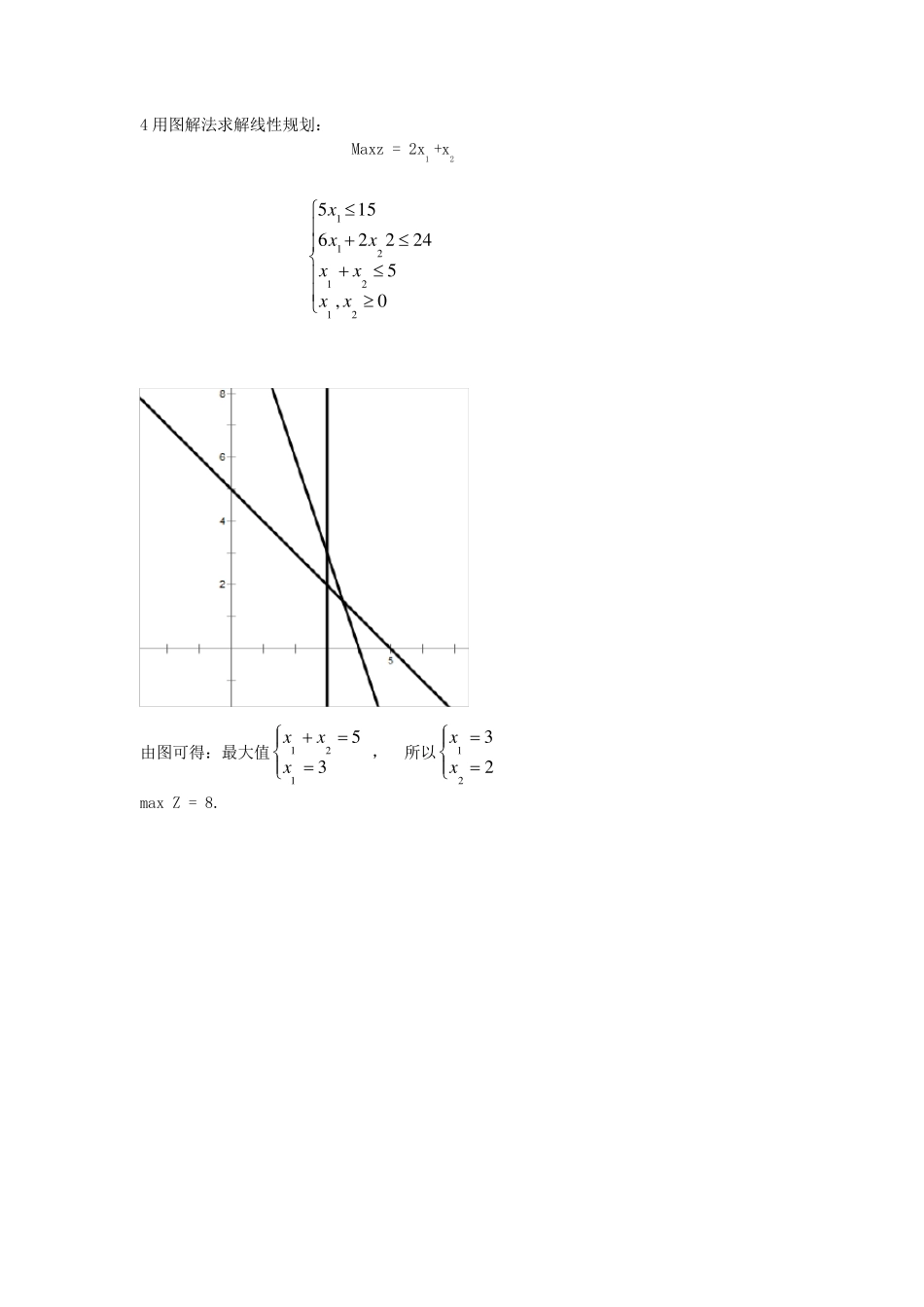
第一章 线性规划 1、 由图可得：最优解为 2、用图解法求解线性规划： Min z=2x1+x2 01058244212121xxxxxx 解： 由图可得：最优解 x=1.6,y=6.4 3 用图解法求解线性规划： Max z=5x1+6x2 0,23222212121xxxxxx 解： 由图可得：最优解Max z=5x1+6x2, Max z= +4 用图解法求解线性规划： Maxz = 2x1 +x2 0,52 42261 552121211xxxxxxx 由图可得：最大值35121xxx ， 所以2321xx max Z = 8. 1212125.max23284164120,1,2maxZ.jZxxxxxxxj如图所示，在（4，2）这一点达到最大值为2 6 将线性规划模型化成标准形式： Min z=x1-2x2+3x3 无约束321321321321,0,052327xxxxxxxxxxxx 解：令Z’=-Z,引进松弛变量 x4  0，引入剩余变量 x5  0，并令x3=x3’-x3’’,其中x3’ 0,x3’’ 0 Max z’=-x1+2x2-3x3’+3x3’’ 0,0,0'',0',0,05232'''7'''5433213215332143321xxxxxxxxxxxxxxxxxxx 7 将线性规划模型化为标准形式 Min Z =x1+2x2+3x3 无约束，321321321321,00632442392-xxxxxxxxxxxx 解：令Z’ = -z，引进松弛变量x4 0,引进剩余变量x5 0,得到一下等价的标准形式。 ,0,,,0632442392-542132153214321xxxxxxxxxxxxxxx x2’=-x2 x3=x3’-x3’’ Z’ = -min Z = -x1-2x2-3x3 632442392-''3'3215''33'214''3'3'21xxxxxxxxxxxxxx 123123412358.maxZ=3x3434540643660,1,2,3,4,5jxxxxxxxxxxxj Cj 3 3 4 0 0 θi CB XB b x1 x2 x3 x4 x5 0 X4 40 3 4 5 1 0 8 0 X5 60 6 4 3 0 1 20 σj 3 3 4 0 0 4 x3 8 3/5 4/5 1 1/5 0 40/3 0 x5 42 21/5 8/5 0 -3/5 1 60/7 σj 3/5 -1/5 0 -4/5 0 4 x3 2 0 4/7 1 4/35 -1/7 3 x1 10 1 8/21 0 1/7 5/21 σj 0 -3/7 0 -31/35 -1/7 10,2,max. 最优解为（0，0,0），目标函数Z=38 9 用单纯形法求解线性规划问题： Max Z...