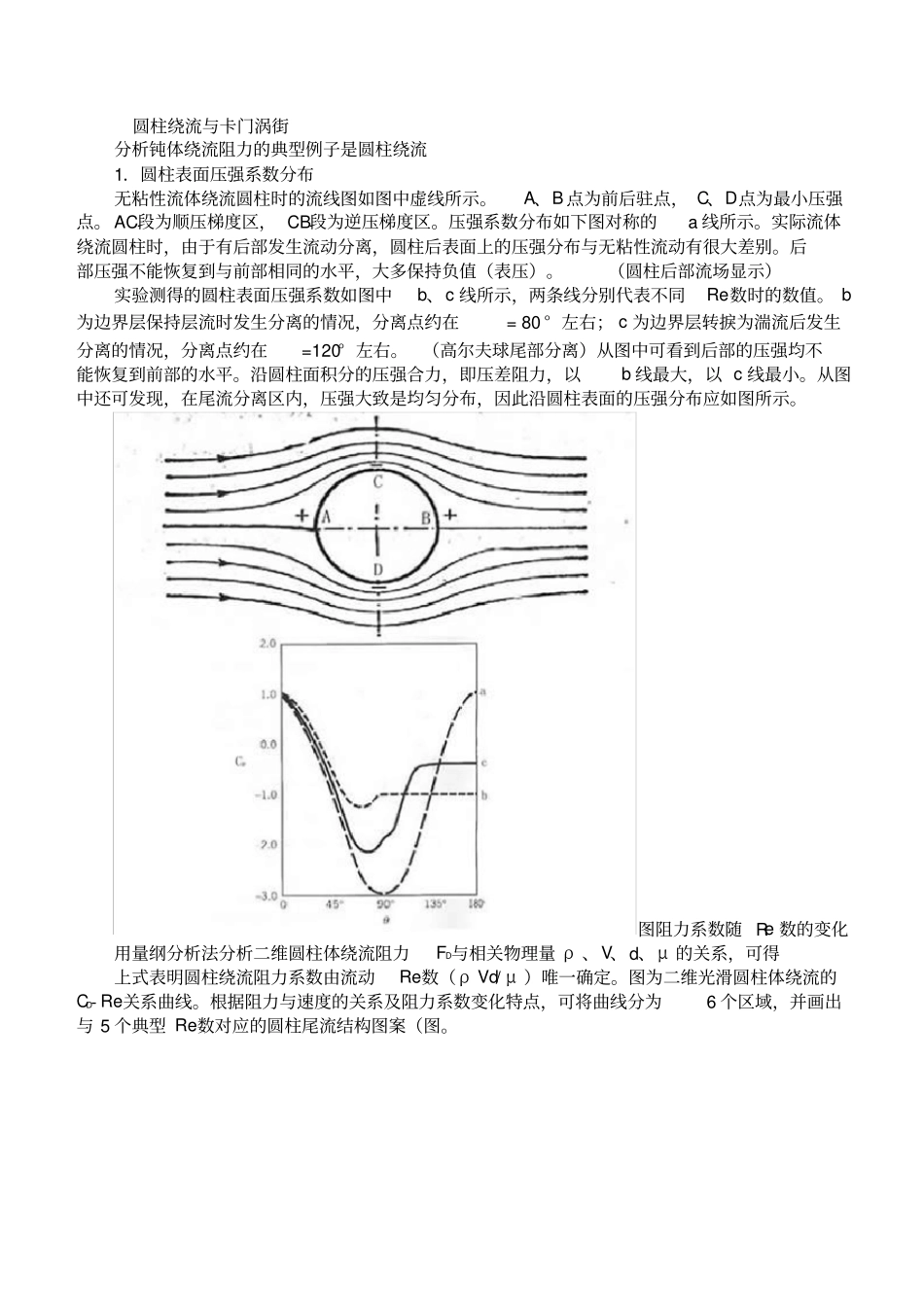
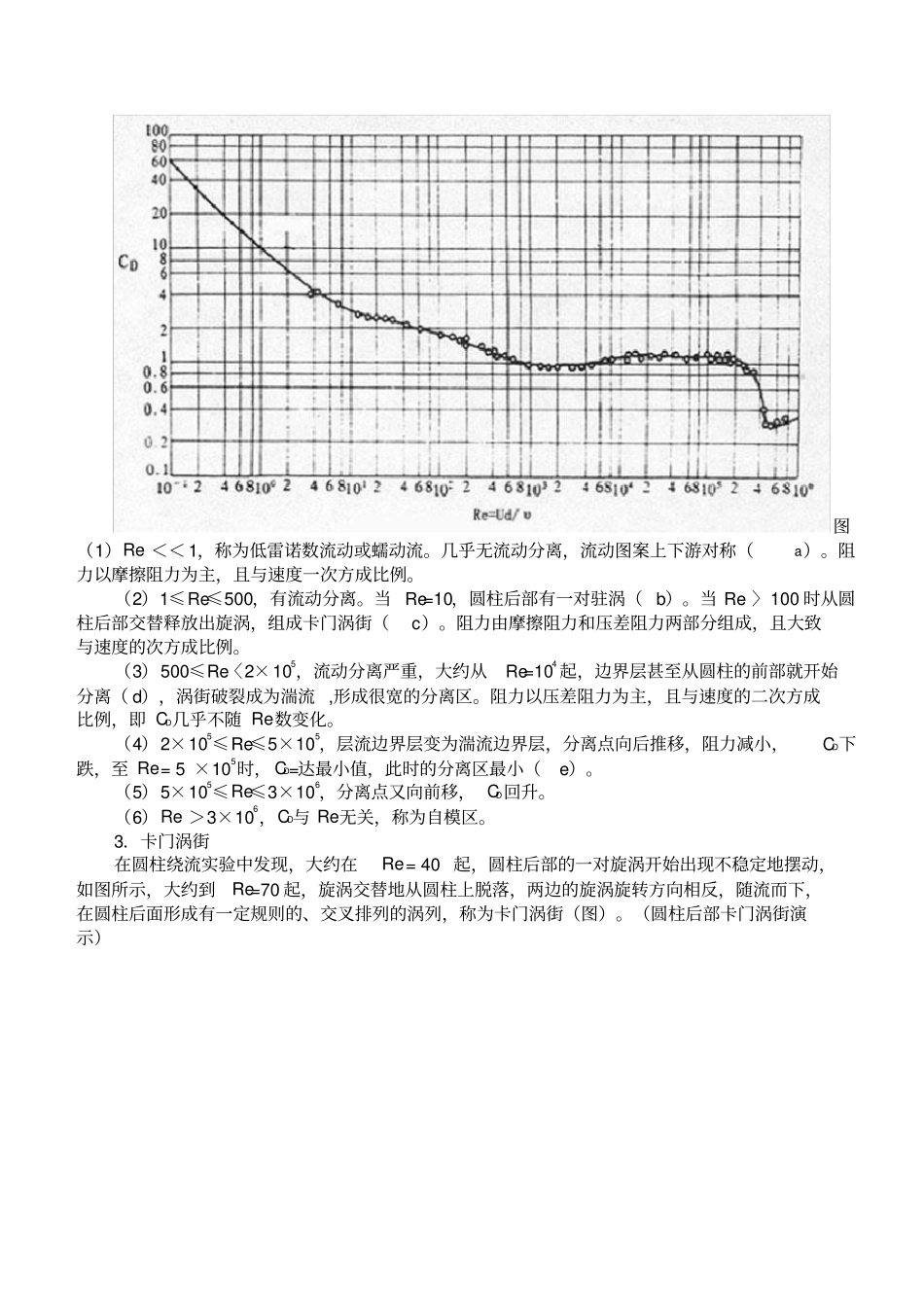
圆柱绕流与卡门涡街分析钝体绕流阻力的典型例子是圆柱绕流1.圆柱表面压强系数分布无粘性流体绕流圆柱时的流线图如图中虚线所示。A、B 点为前后驻点, C、D点为最小压强点。 AC段为顺压梯度区, CB段为逆压梯度区。压强系数分布如下图对称的a 线所示。实际流体绕流圆柱时,由于有后部发生流动分离,圆柱后表面上的压强分布与无粘性流动有很大差别。后部压强不能恢复到与前部相同的水平,大多保持负值(表压)。(圆柱后部流场显示)实验测得的圆柱表面压强系数如图中b、c 线所示,两条线分别代表不同Re数时的数值。 b为边界层保持层流时发生分离的情况,分离点约在= 80 ° 左右; c 为边界层转捩为湍流后发生分离的情况,分离点约在=120° 左右。(高尔夫球尾部分离)从图中可看到后部的压强均不能恢复到前部的水平。沿圆柱面积分的压强合力,即压差阻力,以b 线最大,以 c 线最小。从图中还可发现,在尾流分离区内,压强大致是均匀分布,因此沿圆柱表面的压强分布应如图所示。图阻力系数随 Re 数的变化用量纲分析法分析二维圆柱体绕流阻力FD与相关物理量 ρ 、V、d、μ 的关系,可得上式表明圆柱绕流阻力系数由流动Re数( ρ Vd/ μ )唯一确定。图为二维光滑圆柱体绕流的CD- Re关系曲线。根据阻力与速度的关系及阻力系数变化特点,可将曲线分为6 个区域,并画出与 5 个典型 Re数对应的圆柱尾流结构图案(图。图(1)Re << 1,称为低雷诺数流动或蠕动流。几乎无流动分离,流动图案上下游对称(a)。阻力以摩擦阻力为主,且与速度一次方成比例。(2)1≤Re≤500,有流动分离。当 Re=10,圆柱后部有一对驻涡( b)。当 Re 〉100 时从圆柱后部交替释放出旋涡,组成卡门涡街(c)。阻力由摩擦阻力和压差阻力两部分组成,且大致与速度的次方成比例。(3)500≤Re〈2×105,流动分离严重,大约从Re=104 起,边界层甚至从圆柱的前部就开始分离( d),涡街破裂成为湍流 ,形成很宽的分离区。阻力以压差阻力为主,且与速度的二次方成比例,即 CD几乎不随 Re数变化。(4)2×105≤Re≤5×105,层流边界层变为湍流边界层,分离点向后推移,阻力减小,CD下跌,至 Re = 5 ×105时, CD=达最小值,此时的分离区最小(e)。(5)5×105≤Re≤3×106,分离点又向前移, CD回升。(6)Re >3×106,CD与 Re无关,称为自模区。3.卡门涡街在圆柱绕流实验中发现,大约在Re = 40 起,圆柱后部的一对旋涡开始出...