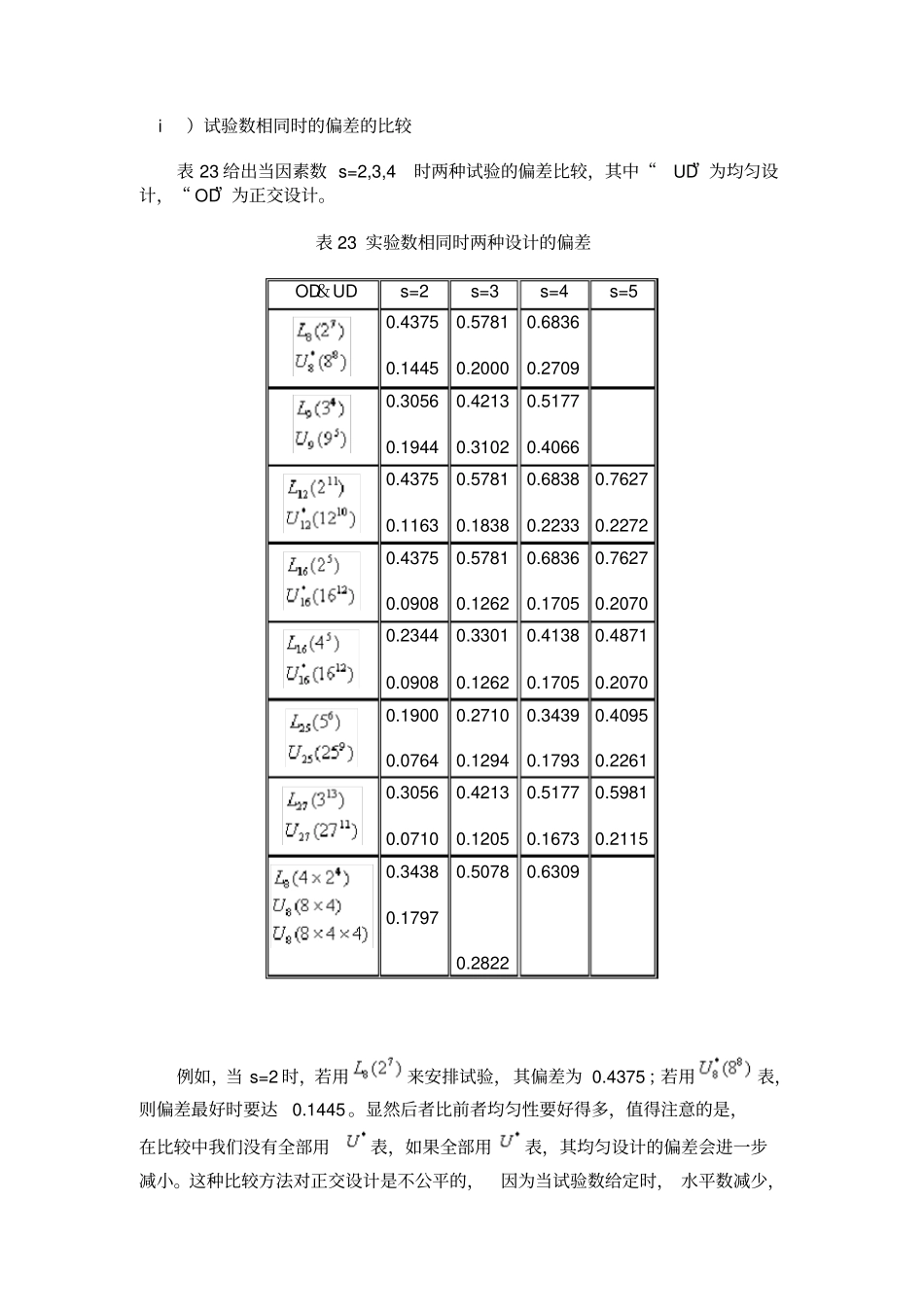
均匀设计和正交设计的比较正交设计和均匀设计是目前最流行的两种试验设计的方法,它们各有所长,相互补充,给使用者提供了更多的选择。本节将讨论两种试验设计的特点。首先正交设计具有正交性,如果试验按它设计,可以估计出因素的主效应,有时也能估出它们的交互效应。均匀设计是非正交设计, 它不可能估计出方差分析模型中的主效应和交互效应, 但是它可以估出回归模型中因素的主效应和交互效应(参见 1.3 节)。正交设计用于水平数不高的试验,因为它的试验数至少为水平数的平方。我们曾遇到一项试验,有五个因素,每个因素取31 水平,其全部组合有个,若用正交设计,至少需要做次试验,而用均匀设计只需 31 次,所以均匀设计适合于多因素多水平试验。均匀设计提供的均匀设计表在选用时有较多的灵活性。例如,一项试验若每个因素取 4 个水平,用来安排,只需作 16 次试验,若改为 5 水平,则需用表,作 25 次试验。从 16 次到 25 次对工业试验来讲工作量有显著地不同。又如在一项试验中, 原计划用均匀设计来安排五个因素, 每个有 13个水平。后来由于某种需要,每个因素改为14 个水平,这时可用来安排,试验次数只需增加一次。 均匀设计的这个性质, 有人称为 “试验次数随水平增加有“ 连续性 ”,并称正交设计“有 跳跃性 ”。正交设计的数据分析程式简单,有一个计算器就可以了, 且“直观分析” 可以给出试验指标 Y 随每个因素的水平变化的规律。 均匀设计的数据要用回归分析来处理, 有时需用逐步回归等筛选变量的技巧,非使用电脑不可。 幸好电脑在我国已日趋普及, 找一台电脑已不是很困难的事。 配合本书,我们已编了一套软件,并有相应的说明。下面我们对两种设计的均匀性作一比较。在 3.2 节我们曾通过线性变换将一个均匀设计表的元素变到( 0,1)中,它的 n 行对应于中的 n 点。用类似的方法, 也可以将表变换为中的 n 点。这两个点集的偏差可以衡量它们的均匀性, 或代表性。 要合理地比较两种设计的均匀性并不容易,因为很难找到二个设计有相同的试验数和相同的水平数,一个来自正交设计, 另一个来自均匀设计。由于这种困难,我们从如下三个角度来比较: i)试验数相同时的偏差的比较表 23 给出当因素数 s=2,3,4 时两种试验的偏差比较,其中“UD”为均匀设计,“ OD”为正交设计。表 23 实验数相同时两种设计的偏差OD&UDs=2s=3s=4s=50.4375 0.1445 0.5781 0.2...