(学案与测评)高考数学总复习 第八单元第四节 基本不等式及其应用精品课件 苏教版 课件VIP免费

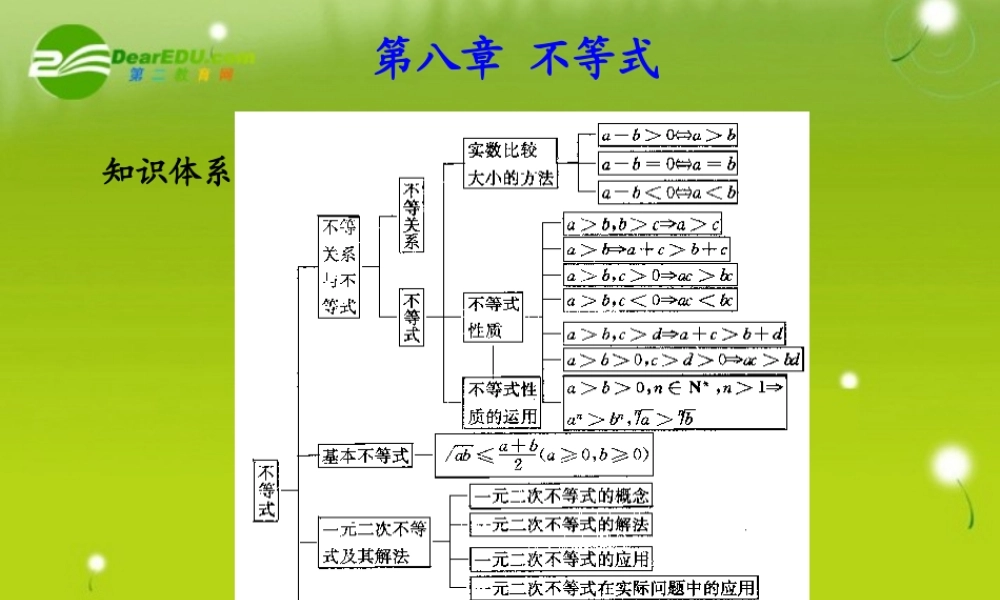
第八章 不等式知识体系 第四节 基本不等式及其应用基础梳理2. 几个重要的不等式(1)a2+b2≥ (a,b∈R).(2) ≥ (a,b 同号 ).(3)ab≤ (a,b∈R).bab a2)2ba( a≥0,b≥0a=b2ab21. 基本不等式 (1) 基本不等式成立的条件 : .(2) 等号成立的条件 : 当且仅当 时取等号 .ab2ab 3. 利用基本不等式求最值问题已知 x>0,y>0, 则(1) 如果积 xy 是定值 p, 那么当且仅当 时 ,x+y 有 值是 .( 简记 : 积定和最小 )( ２ ) 如果和 x+y 是定值 p, 那么当且仅当 时 , xy 有 是 .( 简记 : 和定积最大 )p24p2典例分析题型一 证明不等式【例 1 】已知 a>0,b>0,c>0, 且 a+b+c=1,求证 : ≥9.c1b1a1x=y最小最大x=y 证明 = (a+b+c)+ (a+b+c)+ (a+b+c) =3+ + + + + + = ≥3+2+2+2=9.c1b1a1a1b1c1学后反思 本题如果改为 a>0,b>0,c>0, 求 (a+b+c)· （ ）≥ 9 就比较明显 . 用 a+b+c=1 的条件（ a+b+c ）“隐”去，造成了思考上的困难 , 因此应注意“ 1” 的代换 . 构造基本不等式，使其积为定值，并使得等号同时成立 .abacbabccbca)cbbc()caac()baab(3c1b1a1分析 将 a+b+c=1 代入不等式左边 , 构造基本不等式模型 , 再利用基本不等式证明 . 举一反三1. 设 a ＞ 0,b ＞ 0,c ＞ 0, 求证 : 222abcabcbca  证明 : a ＞ 0,b ＞ 0,∴ 同理 , , ∴ 即 2222aabbabb22bcbc 22caca 222abcabcbca  222222abcabcabcbca  题型二 求最值【例 2 】 (1) 设 00,y>0, 且 x+y=1, 求 的最小值 .3x)3x(8ya4a3y2x8 分析 (1) 由 00,8-3x>0.由于 3x+(8-3x)=8, 可由基本不等式得(2) 原式变为 , 再讨论 a-4 的正负 .(3) 由 , 再用基本不等式求最值 .16]23x)(83x[3x)3x(82 4)4a(4a3yx2xy810)yx)(y2x8() y2x8(y2x8 解 (1) 02>0,∴ ,当且仅当 3x=8-3x, 即 时取等号 ,∴ 当 时 , 的最大值是 4.42823x)(83x3x)3x(8y34x 34x 3x)-3x(8y (2) 显然 a≠4, 当 a>4 时 ,a-4>0,∴ , 当且仅当 时 , 取等号 ;43244)(a4a324)(a4a3a4a3...