(学案与测评)高考数学总复习 第十五单元第三节 数学归纳法精品课件 苏教版 课件VIP免费

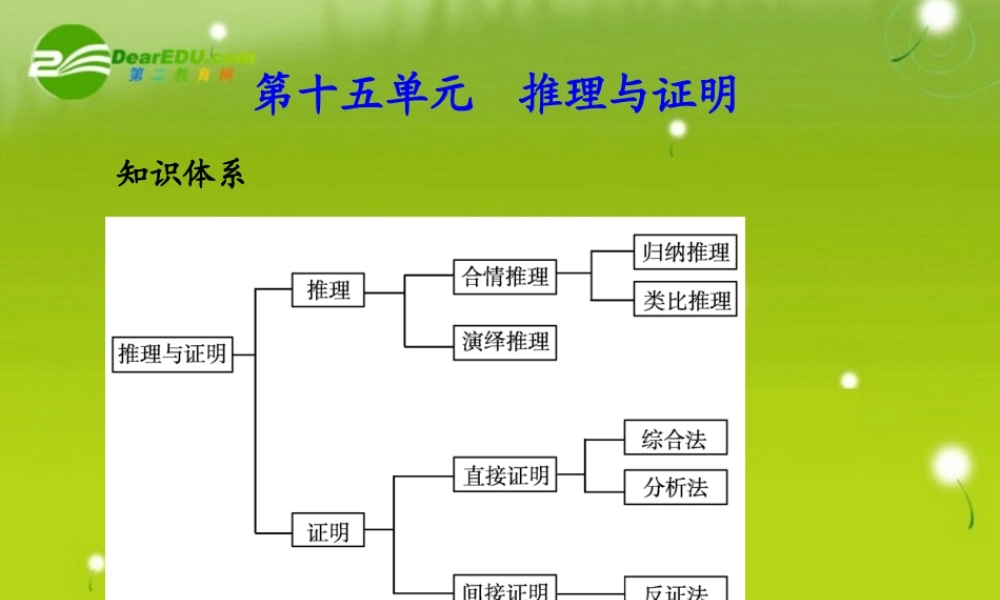
第十五单元 推理与证明知识体系 第三节 数学归纳法 (*)基础梳理1. 数学归纳法的适用对象一般地 , 对于某些与 有关的数学命题 , 我们用数学归纳法公理 .2. 数学归纳法的步骤用数学归纳法证明命题时，其步骤如下：(1) 如果当 n 取第一个值 n0( 例如 n0=1,2 等 ) 时结论正确 ;(2) 假设当 时结论正确 , 证明当 n= 时结论也正确 .那么 , 命题对于从 n0 开始的所有正整数 n 都成立 .正整数n=k(k∈N*, 且 k≥n0)k+1 典例分析题型一 与自然数 n 有关的等式的证明【例 1 】用数学归纳法证明： 分析 用数学归纳法证明问题，应严格按步骤进行，并注意过程的完整性和规范性 .1111...2 44 66 822241nnnn证明 （ 1 ）当 n=1 时，左边 =12×4=18, 右边 =18, 等式成立 .(2) 假设当 n=k(k∈N*) 时 , 成立 ; 1111...2 44 66 822241kkkk 当 n=k+1 时，所以当 n=k+1 时，等式也成立 .综上可得，等式对于任意 n∈N* 都成立 . 11111...2 44 66 822222242114141241211141242411kkkkk kkkkkkkkkkkkkk学后反思 用数学归纳法证题时两个步骤缺一不可，证当 n=k+1 时命题成立，必须要用当 n=k 时成立的结论，否则，就不是数学归纳法证明 . 举一反三1. 求证 : ( 其中 n∈N*).231111111...1222222nnn 证明： (1) 当 n=1 时 , 左边 , 右边 = , 等式成立 .(2) 假设当 n=k 时等式成立 , 即 那么当 n=k+1 时 ,左边 = 这就是说 , 当 n=k+1 时 , 等式也成立 .根据 (1) 、 (2) 可知 , 等式对任何 n∈N* 都成立 .1211122231111111...1222222kkk 2311111111111112 11...1112222222222kkkkkkk   右边 题型二 用数学归纳法证明整除问题【例 2 】求证： （ n∈N* ）能被 9 整除 .31 71nn 分析 当 n=1 时，原式 =27 能被 9 整除 . 因此要研究 与 之间的关系，以便利用归纳假设 能被 9 整除来推证 也能被 9 整除 .31 71kk 134 71kk31 71kk 134 71kk证明 设 （ 1...