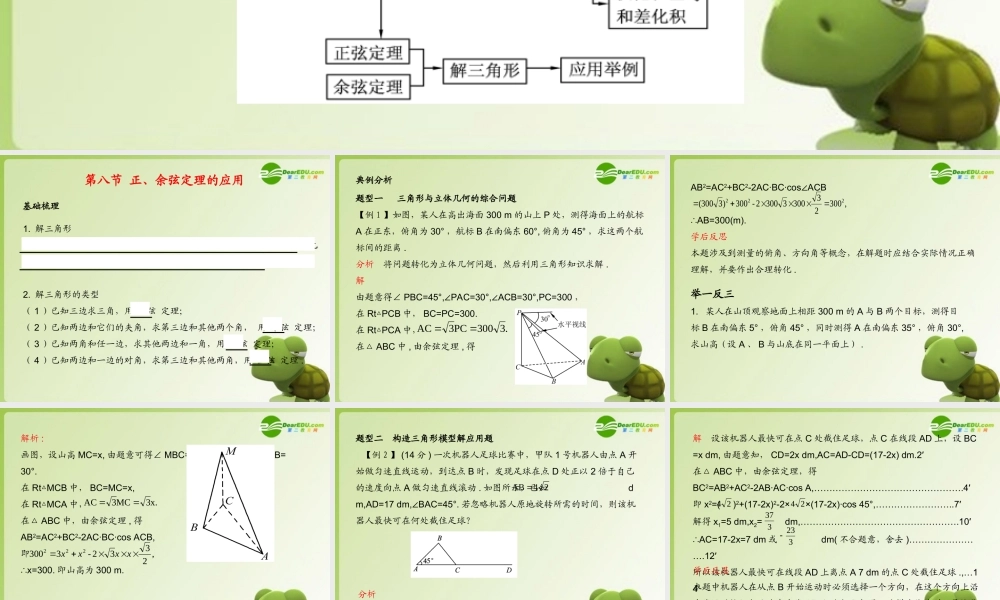
第五单元 基本初等函数Ⅱ知识体系 第八节 正、余弦定理的应用基础梳理1. 解三角形一般地,把三角形三个角 A , B , C 和它们的对边 a,b,c 叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形 .2. 解三角形的类型( 1 )已知三边求三角,用 余弦 定理;( 2 )已知两边和它们的夹角,求第三边和其他两个角, 用 余弦 定理;( 3 )已知两角和任一边,求其他两边和一角,用 正弦 定理;( 4 )已知两边和一边的对角,求第三边和其他两角,用 正弦 定理 . 题型一 三角形与立体几何的综合问题【例 1 】如图,某人在高出海面 300 m 的山上 P 处,测得海面上的航标A 在正东,俯角为 30° ,航标 B 在南偏东 60°, 俯角为 45° ,求这两个航标间的距离 .分析 将问题转化为立体几何问题,然后利用三角形知识求解 .解由题意得∠ PBC=45°, PAC=30°, ACB=30°,PC=300∠∠,在 Rt PCB△中, BC=PC=300.在 Rt PCA△中,在△ ABC 中 , 由余弦定理 , 得典例分析.3300PC3AC AB2=AC2+BC2-2AC·BC·cos ACB∠∴AB=300(m).学后反思本题涉及到测量的俯角、方向角等概念,在解题时应结合实际情况正确理解,并要作出合理转化 .,3002330033002-300)3(300222举一反三1. 某人在山顶观察地面上相距 300 m 的 A 与 B 两个目标,测得目标 B 在南偏东 5° ,俯角 45° ,同时测得 A 在南偏东 35° ,俯角 30°,求山高(设 A 、 B 与山底在同一平面上) . 解析 :画图,设山高 MC=x, 由题意可得∠ MBC=45°, MAC=30°, ACB=∠∠30°.在 Rt MCB△中, BC=MC=x,在 Rt MCA△中,在△ ABC 中,由余弦定理 , 得AB2=AC2+BC2-2AC·BC·cos ACB,即∴x=300. 即山高为 300 m.x.3MC3AC,2332-3300222xxxx 题型二 构造三角形模型解应用题 【例 2 】 (14 分 ) 一次机器人足球比赛中,甲队 1 号机器人由点 A 开始做匀速直线运动,到达点 B 时,发现足球在点 D 处正以 2 倍于自己的速度向点 A 做匀速直线滚动 . 如图所示,已知 dm,AD=17 dm, BAC=45°.∠若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?24AB 分析“ 最快截住”是指“机器人从点 B 沿直线运动时和足球在直线 AD 上的点 C 处相遇”,此时 CD=2BC ,将问题归结到△ ABC 中,用余弦定理解决 . ...