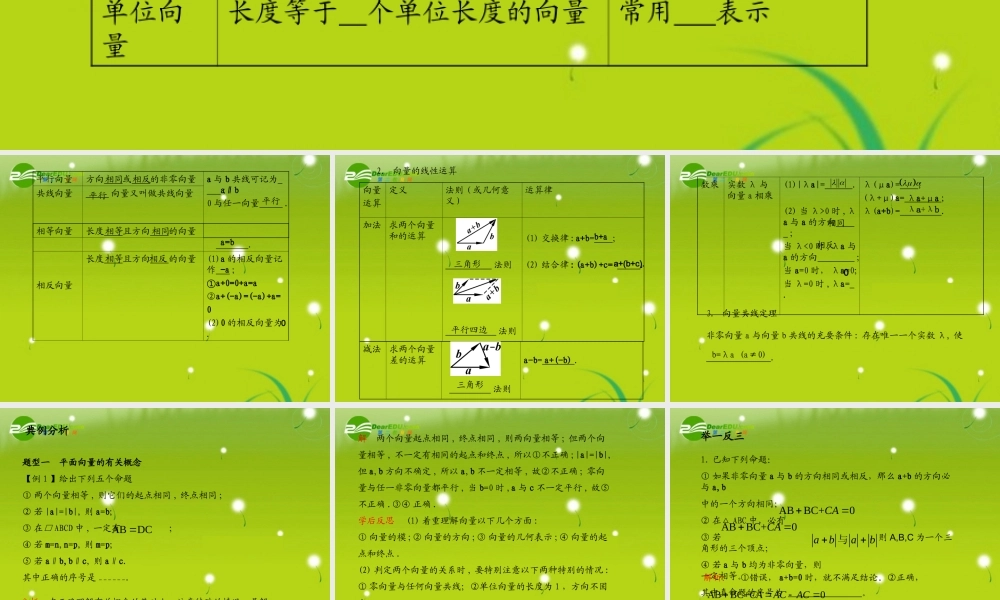
第一节 平面向量的概念及其线性运算基础梳理1. 向量的有关概念及表示法名称定义表示法向量既有 又有 的量 ; 向量的大小叫做向量的 ( 或 )向量 .模 .零向量长度为 的向量 ; 其方向是任意的记作 .单位向量长度等于 个单位长度的向量常用 表示大小方向长度模AB�AB�001e平行向量方向 或 的非零向量a 与 b 共线可记为 ;0 与任一向量 .共线向量 向量又叫做共线向量相同相反平行a∥b平行相等向量长度 且方向 的向量 .相反向量长度 且方向 的向量(1)a 的相反向量记作 ;①a+0=0+a=a②a+(-a)=(-a)+a=0(2)0 的相反向量为 .相等相同a=b相等相反-a02. 向量的线性运算向量运算定义法则 ( 或几何意义 )运算律加法求两个向量和的运算 法则 法则(1) 交换律 :a+b= ;(2) 结合律 :(a+b)+c= .减法求两个向量差的运算 法则a-b= .b+aa+(b+c).三角形平行四边三角形a+(-b)数乘实数 λ 与向量 a 相乘(1)|λa|= .(2) 当 λ>0 时 ,λa 与 a 的方向 ;当 λ<0 时 ,λa 与a 的方向 ;当 a=0 时, λa=0;当 λ=0 时 ,λa= .λ(μa)= ;(λ+μ)a= ;λ(a+b)= .3. 向量共线定理非零向量 a 与向量 b 共线的充要条件 : 存在唯一一个实数 λ, 使 .b=λa (a≠0) 相同相反0 λa+μaλa+λb典例分析题型一 平面向量的有关概念【例 1 】给出下列五个命题① 两个向量相等 , 则它们的起点相同 , 终点相同 ;② 若 |a|=|b|, 则 a=b;③ 在□ ABCD 中 , 一定有 ;④ 若 m=n,n=p, 则 m=p;⑤ 若 a∥b,b∥c, 则 a∥c.其中正确的序号是 ______.ABDC�分析 在正确理解有关概念的基础上 , 注意特殊的情况 , 是解决本题的关键 .解 两个向量起点相同 , 终点相同 , 则两向量相等 ; 但两个向量相等 , 不一定有相同的起点和终点 , 所以①不正确 ;|a|=|b|,但 a,b 方向不确定 , 所以 a,b 不一定相等 , 故②不正确 ; 零向量与任一非零向量都平行 , 当 b=0 时 ,a 与 c 不一定平行 , 故⑤不正确 .③④ 正确 .学后反思 (1) 着重理解向量以下几个方面 :① 向量的模 ;② 向量的方向 ;③ 向量的几何表示 ;④ 向量的起点和终点 .(2) 判定两个向量的关系时 , 要特别注意以下两种特别的情况 :① 零向量与任何向量共线;②单位向量的长度为 1 ,方向不固定 .举一反三1. 已知下列命题:① 如果非零向量 a 与 b ...