(学案与测评)高考数学总复习 第九单元第六节 椭圆精品课件 苏教版 课件-2VIP免费

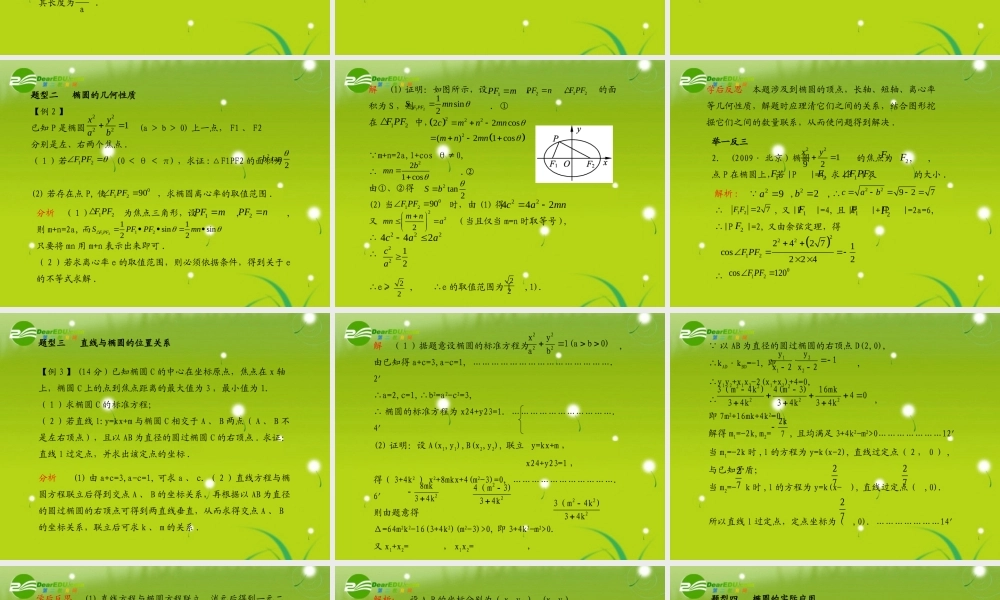
第六节 椭圆基础梳理1. 椭圆的定义（ 1 ）平面内的动点的轨迹是椭圆必须满足的两个条件 :① 到两个定点 F1 、 F2 的距离的和等于常数 2a;②2a F1F2.(2) 上述椭圆的焦点是 ，椭圆的焦距是 F1F2.2. 椭圆的标准方程和几何性质＞F1 、F2标准方程 图形性质 范围 ≤x≤a ≤y≤b ≤x≤b ≤y≤a对称性 对称轴 : 坐标轴 对称中心 : 原点 顶点 A1 ,A2B1 ,B2 A1 ,A2B1 ,B2 轴 长轴 A1A2 的长为 短轴 B1B2 的长为 .焦距 F1F2=离心率 e= ∈a,b,c的关系 c2=0)b1(abyax22220)b1（abxay2222ac-a-a-b-b(-a,0)(0,-b)(a,0)(0,b)(0,-a)(-b,0)(0,a)(b,0)2a2b2c(0,1)a2-b2典例分析题型一 椭圆的定义及其标准方程【例 1 】已知 P 点在以坐标轴为对称轴的椭圆上，点 P 到两焦点的距离分别为 和 ，过 P 作长轴的垂线恰好过椭圆的一个焦点，求此椭圆的方程 .分析 方法一：用待定系数法，设出椭圆方程的两种形式后，代入求解 .方法二：先由椭圆定义，确定半长轴 a 的大小，再在直角三角形中，利用勾股定理求 c, 然后求 b.354352解 方法一：设椭圆的标准方程 或 , 两个焦点分别为 F1 、 F2 ，则由题意知2a=PF1+PF2= , ∴a= .在方程 中 , 令 x=±c, 得｜ y ｜ = ；在方程 中 , 令 y=±c, 得｜ x ｜ = .依题意知 = ,∴b2= .即椭圆的方程为0)b1(abyax22220)b1（abxay22225251byax22221bxay2222ab2ab2ab21103x5y1或103y5x2222532310方法二：设椭圆的两个焦点分别为 F1 、 F2, 则PF1= ,PF2= .由椭圆的定义 , 知 2a=PF1+PF2= , 即 a= .354352525由 PF1>PF2 知， PF2 垂直于长轴 .故在 Rt△PF2F1 中， 4c2=PF12-PF22= ,∴c2=53 ，于是 b2=a2-c2= .又所求椭圆的焦点可以在 x 轴上，也可以在 y 轴上，故所求的椭圆方程为学后反思 (1) 用待定系数法求椭圆方程时，当题目的条件不能确定椭圆的焦点位置时，应注意分两种情况来设方程，分别计算；有时也可以直接设成（ 2 ）过椭圆焦点与长轴垂直的直线截椭圆的弦通常叫做通径，其长度为 .9603101103x5y1或103y5x22220)n0,1(mnymx22a2b2举一反三1. 已知椭圆的中心在原点，焦点在坐标轴上，长轴长是短轴长的 3 倍，且过点 P(3,2), 求椭圆的方程 .解析 : （ 1 ）当焦点在 x 轴上时，设椭圆方程为 (a ＞ b ＞ 0),则 ...