(学案与测评)高考数学总复习 第十二单元第三节 二项式定理精品课件 苏教版 课件VIP免费

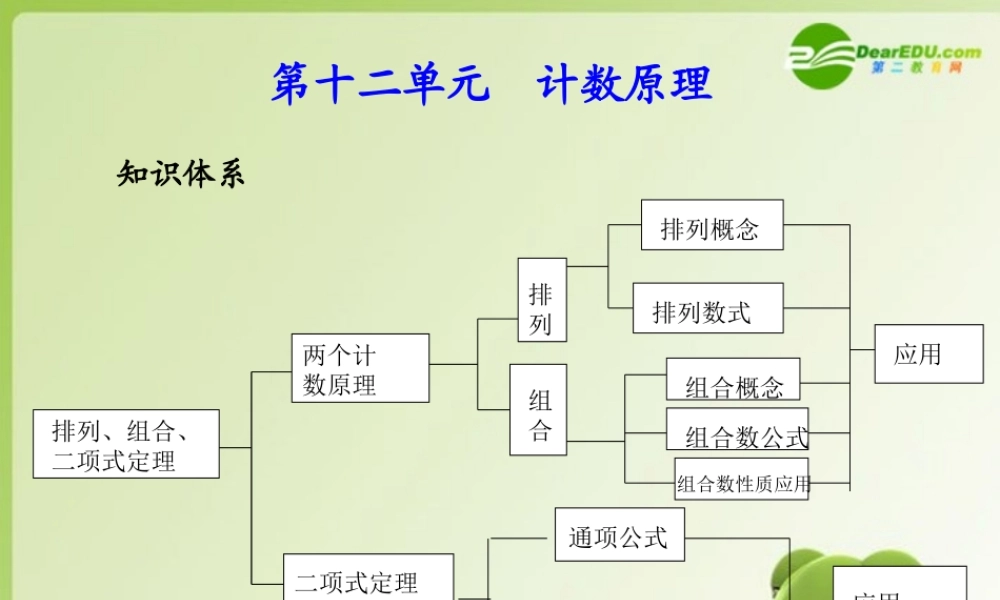
排列、组合、二项式定理两个计数原理 二项式定理排列组合排列概念排列数式组合概念 组合数公式组合数性质应用通项公式二项式系数性质应用应用第十二单元 计数原理知识体系 第三节 二项式定理 (*)基础梳理011......nnrn rrnnnnnnC aC abC abC b11......rrnnnC xC xxrn rrnC ab0122......nrnnnnnnCCCCC1nxnab1. 二项式定理及其特例(1) = ;(2) = .特别是当 x=1 时，得 .2. 二项展开式的通项公式 = (r=0,1,2,…,n).3. 二项式系数表（杨辉三角） 展开式的二项式系数，当 n 依次取 1,2,3,… 时，二项式系数表中每行两端都是 1 ，除 1 以外的每一个数都等于 .1rT nab它肩上两个数的和 4. 二项式系数 的性质(1) ;(2) ;(3) 当 时 , ; 当 时， ;(4) .01,,...,nnnnCCCmn mnnCC 11mmmnnnCCC12nr1rrnnCC 12nr1rrnnCC 012...2nnnnnnCCCC 典例分析解 展开式通项 .由题意得 (r=0,1,2,…,n),故当 r=2 时，正整数的最小值为 5.225132332rn rn rrrn rnrrnnTCxCxx 52502nrnr 题型一 求二项式 中的 n【例 1 】如果 的展开式中含有非零常数项，则正整数 n 的最小值为 .分析根据展开式中含有非零常数项，求得 n,r 之间的关系，从而求出 n.2323nxxnab 学后反思 常数项即变量的指数为 0 ，有理项即变量的指数为整数，这都是列方程的依据，根据方程求得关系，再解题 .答案： 3 举一反三1. （ 2009· 济南模拟）若二项式 的展开式中存在常数项，则正整数 n 的最小值等于 .1nxx解析： 二项展开式的通项公式为 由二项展开式中存在常数项，可令 n-3r=0, n∈N*,r∈N*, 且 r≤n, 则使得 n-3r=0 的正整数 n 的最小值为 3.3211nrn rrrrrrnnCxxCx 题型二 求项的系数【例 2 】 展开式中 的系数为 . 34121xx2x分析 利用通项公式分别写出常数项、含 x, 项，从而求出系数 .2x解 展开式中 项为 ∴ 所求系数为  34121xx0 302221 211 312220403434341 (2 )1 ()1 (2 )1 ()1 (2 )1 ()CxCxCxCxCxCx0211220343434212624 126C CCCCC  2x 学后反...