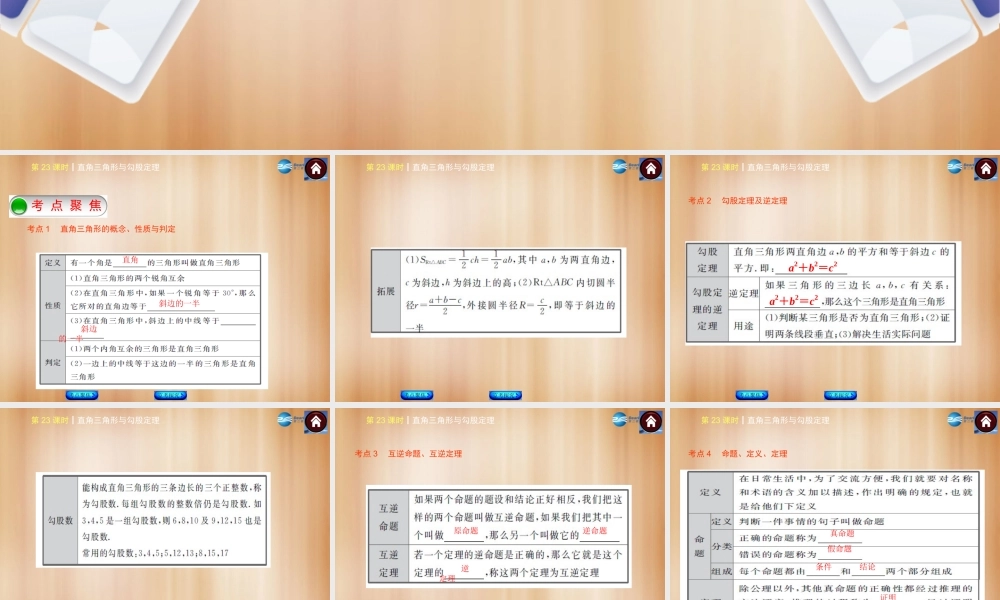
第 23 课时 直角三角形与勾股定理京 考 探 究京 考 探 究考 点 聚 焦考 点 聚 焦考 点 聚 焦考点 1 直角三角形的概念、性质与判定考点聚焦京考探究第 23 课时┃直角三角形与勾股定理直角斜边的一半斜边的一半第 23 课时┃直角三角形与勾股定理考点聚焦京考探究考点 2 勾股定理及逆定理第 23 课时┃直角三角形与勾股定理a2+b2=c2 a2+b2=c2 考点聚焦京考探究第 23 课时┃直角三角形与勾股定理考点聚焦京考探究考点 3 互逆命题、互逆定理第 23 课时┃直角三角形与勾股定理原命题逆命题逆定理考点聚焦京考探究考点 4 命题、定义、定理第 23 课时┃直角三角形与勾股定理真命题假命题条件结论证明定理考点聚焦京考探究 考 情 分 析京 考 探 究第 23 课时┃直角三角形与勾股定理考点聚焦京考探究热考一 直角三角形的性质与判定热 考 京 讲第 23 课时┃直角三角形与勾股定理例 1 如图 23-1 所示,已知△ABC 中,AB=5 cm,BC=12 cm,AC=13 cm,那么 AC 边上的中线 BD 的长为________ cm. 132 考点聚焦京考探究第 23 课时┃直角三角形与勾股定理[解析] 由勾股定理逆定理, 52+122=132,∴△ABC 为直角三角形,AC 为斜边. BD 为斜边AC 边上的中线,∴BD=12AC=132 . 考点聚焦京考探究 思想方法第 23 课时┃直角三角形与勾股定理(1)勾股定理的逆定理常用来判别三角形是否为直角三角形,应用非常广泛.在应用中要善于观察勾股数的存在,以便尽快确定三角形的形状,进行求解.常见的勾股数有 3,4,5;5,12,13;8,15,17. (2)直角三角形斜边上的中线等于斜边的一半.反之也成立,即如果三角形中一边上的中线等于这条边的一半,那么这个三角形为直角三角形. 考点聚焦京考探究第 23 课时┃直角三角形与勾股定理已知三角形 ABC 为直角三角形,且两条边长分别为 3 厘米与 4 厘米,则斜边上的中线长为________________. 变式题2.5 厘米或 2 厘米 考点聚焦京考探究 思想方法第 23 课时┃直角三角形与勾股定理分类讨论思想——直角三角形的边 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边 4 既可以是直角边,也可以是斜边,所以求斜边上的中线长必须分类讨论,即 4 是斜边和直角边这两种情况,然后利用勾股定理求解.而此题接着考查了斜边上的中线等于斜边的一半,进而求出斜边上的中线长为 2...