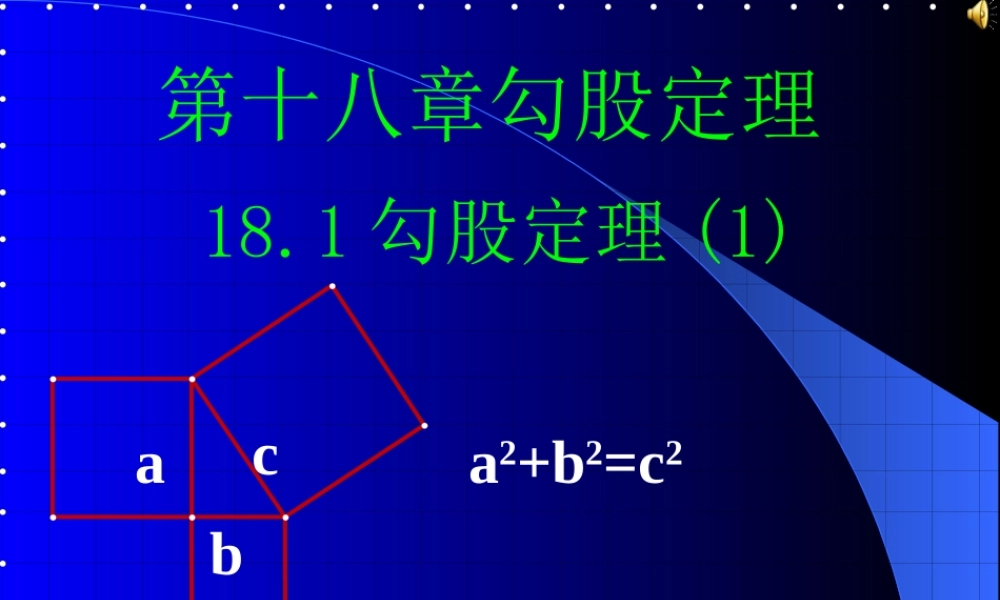
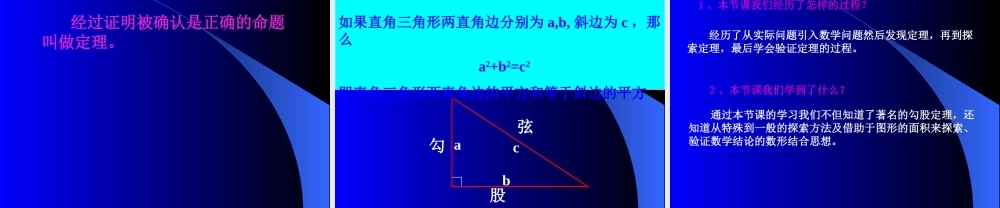
第十八章勾股定理baca2+b2=c218.1 勾股定理 (1) 左下图是 2002 年在北京召开的国际数学家大会会徽 数学家毕达哥拉斯的故事A 、 B 、 C 的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方探究一ABC 相传 2005 年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某中数量关系。 图 1—2ABC( 1 )观察图 1—2 :正方形 A 中含有 个小方格,即 A 的面积是 个单位面积;正方形 B 中含有 个小方格,即 B 的面积是 个单位面积;正方形 C 中含有 个小方格,即 C 的面积是 个单位面积;444488A 的面积 + B 的面积 = C 的面积 ABC图 1—1( 2 )观察图 1—1 :正方形 A 中含有 个小方格,即 A 的面积是 个单位面积;正方形 B 中含有 个小方格,即 B 的面积是 个单位面积;正方形 C 中含有 个小方格,即 C 的面积是 个单位面积;99991818A 的面积 + B 的面积 = C 的面积 对于等腰直角三角形有这样的性质:对于任意直角三角形都有这样的性质吗?两直边的平方和等于斜边的平方看下图 ABCA 的面积 ( 单位长度 )B 的面积 ( 单位长度 )C 的面积 ( 单位长度 )图 2图 3A 、 B 、C 面积关系直角三角形三边关系图 2图 3491392534sA+sB=sC两直角边的平方和等于斜边的平方ABC探究二:你会求出三角形的面积吗? baca2+b2=c2正方形 A 中含有 个方格,即 A 的面积是 个单位面积;正方形 B 中含有 个小方格,即 B 的面积是 个单位面积;正方形 C 中含有 个小方格,即 C 的面积 个单位面积;9916162525BAC ca b c2 = (a b)2 + 4(½ab)= a2 2ab + b2 + 2ab c2 = a2 + b2依据科学理论的证实:一 33 世纪我国汉代的赵爽指出:四个全等的直角三世纪我国汉代的赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与等于小正方形的面积与 44 个三角形的面积和得: 个三角形的面积和得: 两直角边的平方和等于斜边的平方赵爽弦图 “ 赵爽弦图”表现了我国古代人对数学的钻研精神和聪明才智,它是我国数学的骄傲。 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是...