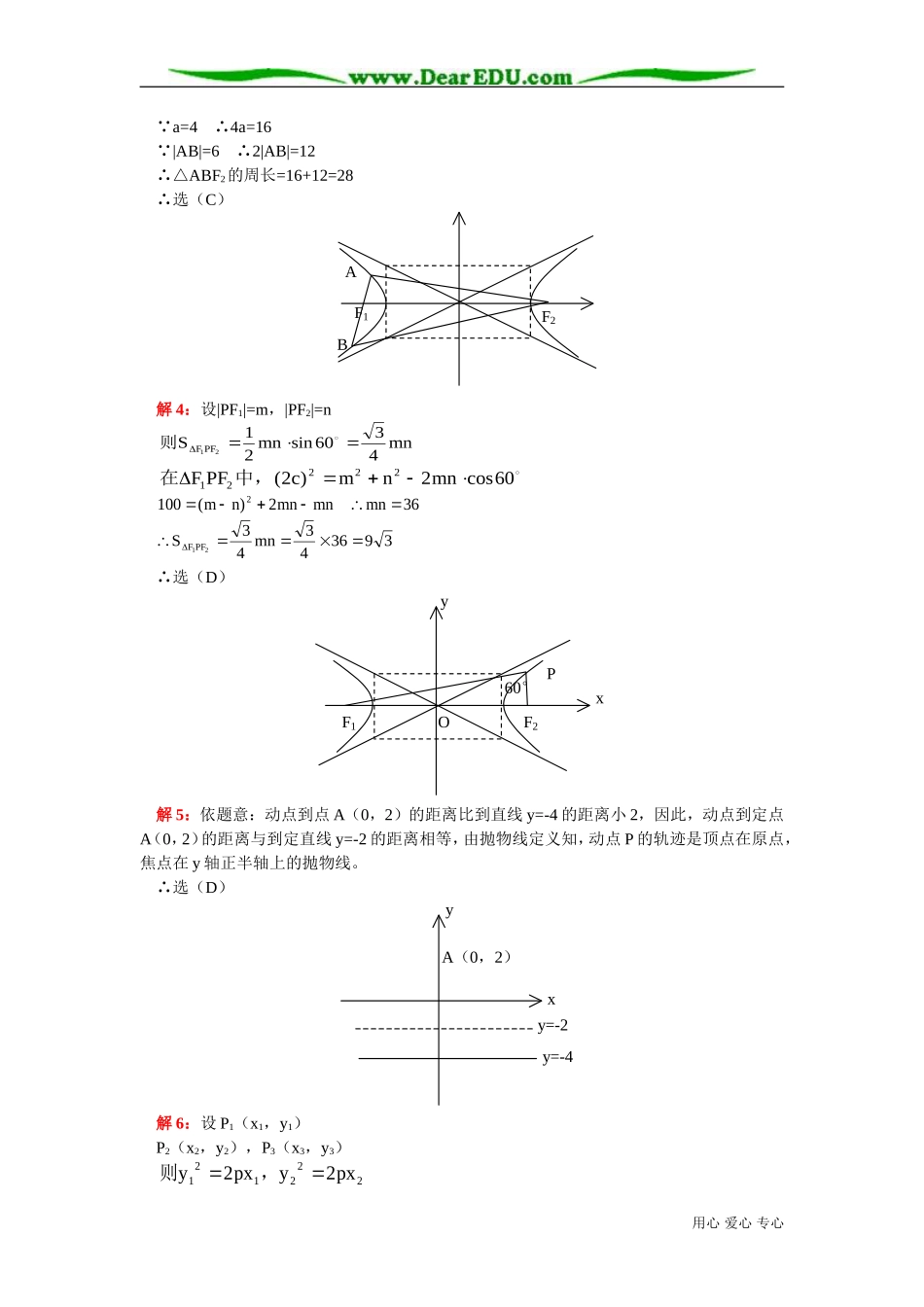
高二数学利用圆锥曲线的定义解题知识精讲 人教版一. 本周教学内容: 专题讲座 《利用圆锥曲线的定义解题》二. 复习: 椭圆、双曲线、抛物线、圆锥曲线的统一定义。 1. 椭圆的第一定义: 平面内与两个定点 F1、F2的距离的和等于常数 2a(a>0),(2a>|F1F2|)的点的轨迹叫椭圆。 注: (1)2a>|F1F2|时,动点的轨迹是椭圆; (2)2a=|F1F2|时,动点的轨迹是线段; (3)2a<|F1F2|时,动点无轨迹。 2. 椭圆的第二定义: 平面内与一个定点的距离和到一条定直线的距离的比是常数 e(0|F1F2|时,动点无轨迹。 4. 双曲线的第二定义: 平面内与一个定点的距离和到一条定直线的距离的比是常数 e(e>1)的点的轨迹叫双曲线。定点是双曲线的焦点,定直线叫双曲线的准线,常数 e 叫双曲线的离心率。 5. 抛物线的定义: 平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫抛物线,定点 F 叫抛物线的焦点,定直线 l 叫抛物线的准线。(要求定点 F 不在定直线 l 上)。 6. 圆锥曲线的统一定义: 平面内与一个定点 F 和一条定直线 l 的距离之比等于常数 e 的动点的轨迹。 (1)当 01 时,表示双曲线。 这三种曲线合在一起,称为圆锥曲线。三. 典型例题分析: 例 1. 选择题 19251122212. FFxyABFABF、是椭圆的两个焦点,是过的弦,则的周长是( ) A. 10 B. 12 C. 20 D. 16 用心 爱心 专心225912 522..椭圆上一点 到左准线的距离为,则点 到右焦点的距离为xyPP( ) 31691221.||双曲线方程为,过左焦点的弦交左支于 、 两点,且xyFABABAB=6,设 F2是右焦点,则△ABF2的周长为( ) A. 16B. 22C. 28D. 32 4169160221212. 双曲线上一点 ,、是双曲线的焦点,且,则xyPFFF PF△F1PF2的面积为( ) 5. 动点 P 到点 A(0,2)的距离比到直线 l:y=-4 的距离小 2,则动点 P 的轨迹方程是( ) A. y2=4xB. y2=8x C. x2=4yD. x2=8y 6. ...