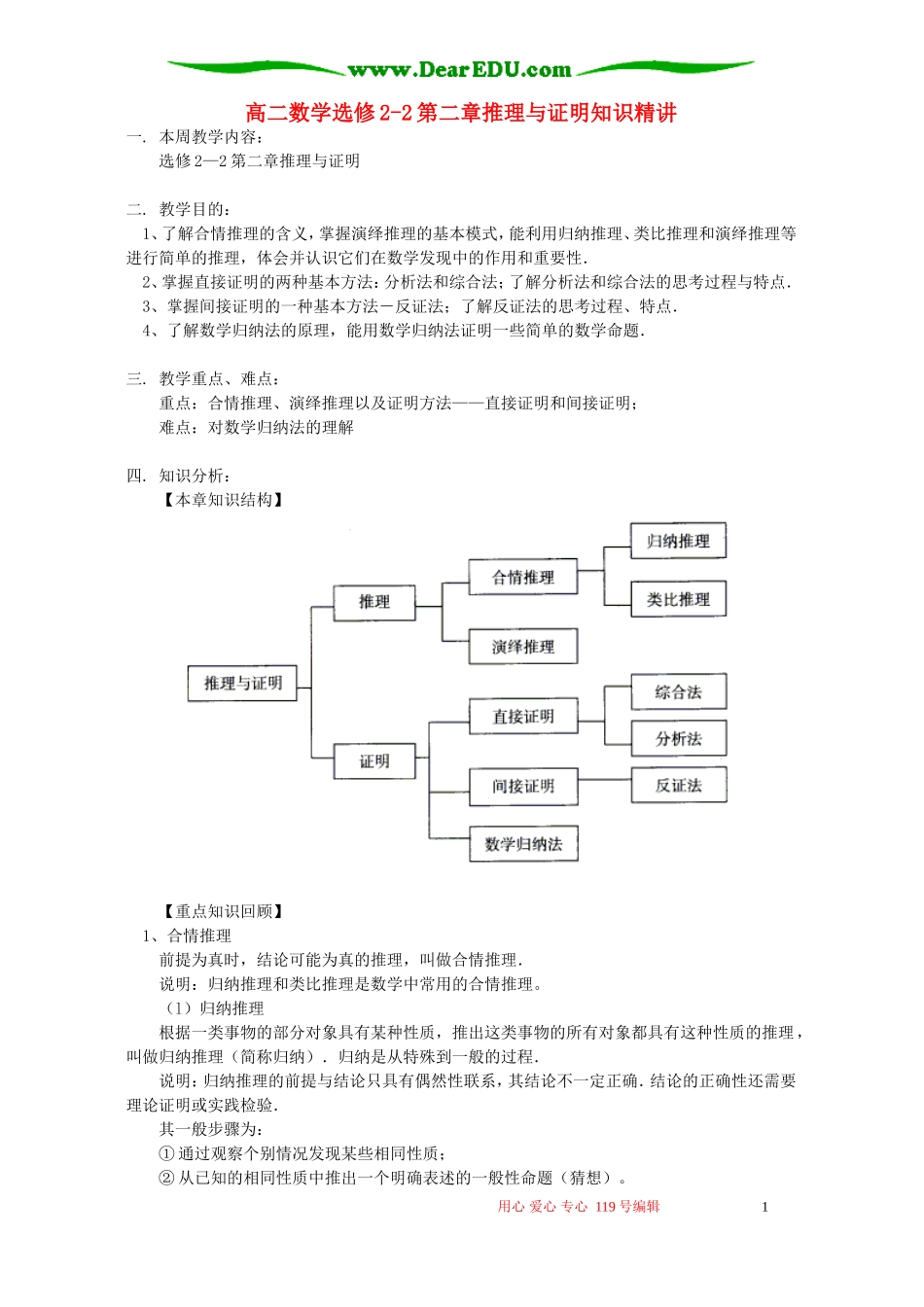
高二数学选修 2-2 第二章推理与证明知识精讲一. 本周教学内容:选修 2—2 第二章推理与证明二. 教学目的:1、了解合情推理的含义,掌握演绎推理的基本模式,能利用归纳推理、类比推理和演绎推理等进行简单的推理,体会并认识它们在数学发现中的作用和重要性.2、掌握直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程与特点.3、掌握间接证明的一种基本方法―反证法;了解反证法的思考过程、特点.4、了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.三. 教学重点、难点:重点:合情推理、演绎推理以及证明方法——直接证明和间接证明;难点:对数学归纳法的理解四. 知识分析:【本章知识结构】【重点知识回顾】1、合情推理前提为真时,结论可能为真的推理,叫做合情推理.说明:归纳推理和类比推理是数学中常用的合情推理。(l)归纳推理根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理,叫做归纳推理(简称归纳).归纳是从特殊到一般的过程.说明:归纳推理的前提与结论只具有偶然性联系,其结论不一定正确.结论的正确性还需要理论证明或实践检验.其一般步骤为:① 通过观察个别情况发现某些相同性质;② 从已知的相同性质中推出一个明确表述的一般性命题(猜想)。用心 爱心 专心 119 号编辑 1 (2)类比推理根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另一类事物类似(或相同)的性质的推理,叫做类比推理(简称类比)。说明:在一般情况下,如果类比的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的命题就越可靠.类比推理的一般步骤为:① 找出两类事物之间的相似性或一致性;② 用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想)。2、演绎推理根据一般性的真命题(或逻辑规则)导出特殊性命题为真的推理,叫做演绎推理.演绎推理的特征是:当前提为真时,结论必然为真.例如,由真命题 a,b,遵循演绎推理规则得出命题 q,则 q 必然为真.3、合情推理与演绎推理的区别归纳和类比是常用的合情推理.从推理形式上看,归纳是由部分到整体,个别到一般的推理,类比是由特殊到特殊的推理,而演绎推理是由一般到特殊的推理.从推理所得的结论来看,合情推理的结论不一定正确,有待进一步证明;演绎推理在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确.4、证明(l)...