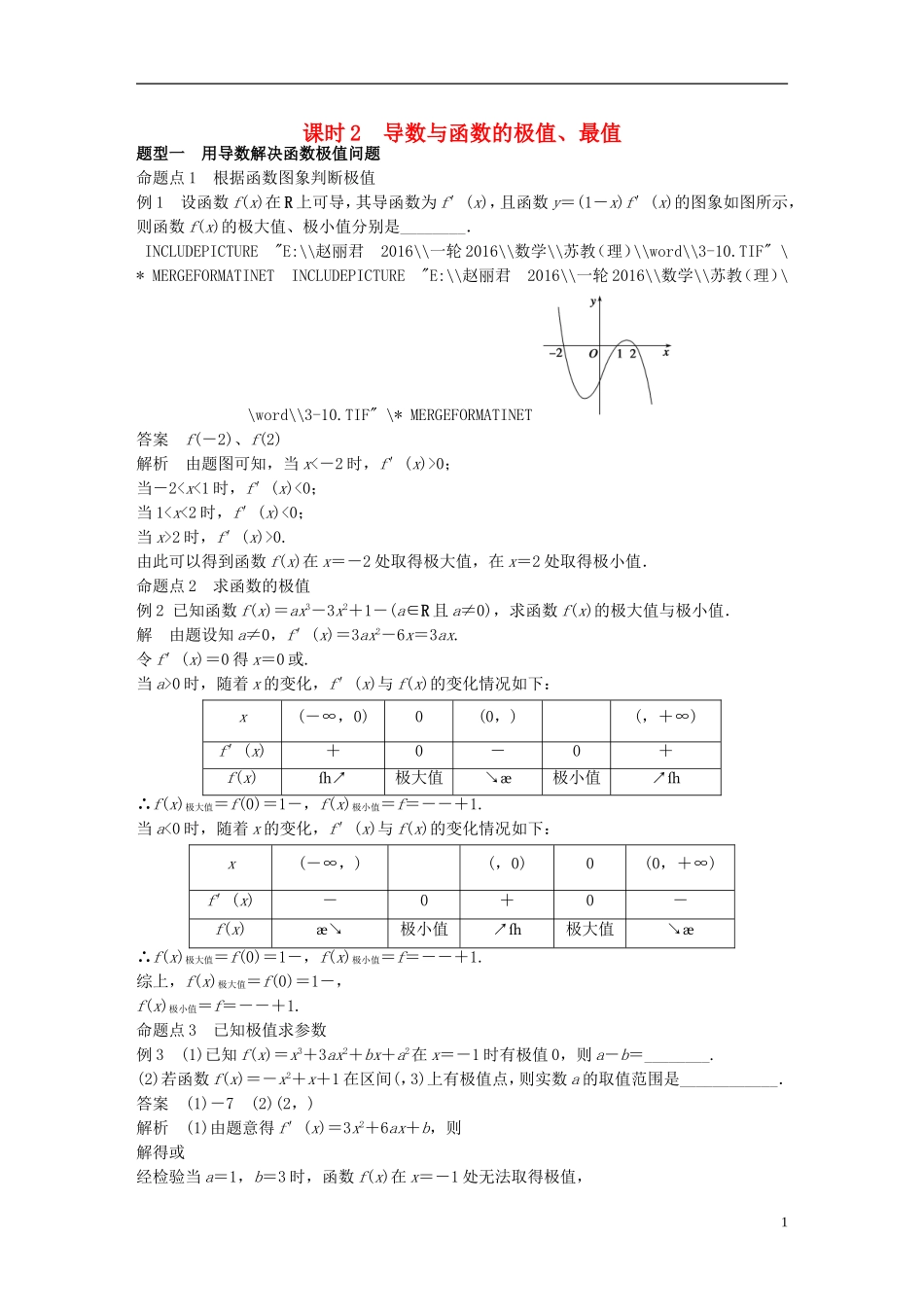
课时 2 导数与函数的极值、最值题型一 用导数解决函数极值问题命题点 1 根据函数图象判断极值例 1 设函数 f(x)在 R 上可导,其导函数为 f′(x),且函数 y=(1-x)f′(x)的图象如图所示,则函数 f(x)的极大值、极小值分别是________. INCLUDEPICTURE "E:\\赵丽君 2016\\一轮 2016\\数学\\苏教(理)\\word\\3-10.TIF" \* MERGEFORMATINET INCLUDEPICTURE "E:\\赵丽君 2016\\一轮 2016\\数学\\苏教(理)\\word\\3-10.TIF" \* MERGEFORMATINET 答案 f(-2)、f(2)解析 由题图可知,当 x<-2 时,f′(x)>0;当-22 时,f′(x)>0.由此可以得到函数 f(x)在 x=-2 处取得极大值,在 x=2 处取得极小值.命题点 2 求函数的极值例 2 已知函数 f(x)=ax3-3x2+1-(a∈R 且 a≠0),求函数 f(x)的极大值与极小值.解 由题设知 a≠0,f′(x)=3ax2-6x=3ax.令 f′(x)=0 得 x=0 或.当 a>0 时,随着 x 的变化,f′(x)与 f(x)的变化情况如下:x(-∞,0)0(0,)(,+∞)f′(x)+0-0+f(x)↗极大值↘极小值↗∴f(x)极大值=f(0)=1-,f(x)极小值=f=--+1.当 a<0 时,随着 x 的变化,f′(x)与 f(x)的变化情况如下:x(-∞,)(,0)0(0,+∞)f′(x)-0+0-f(x)↘极小值↗极大值↘∴f(x)极大值=f(0)=1-,f(x)极小值=f=--+1.综上,f(x)极大值=f(0)=1-,f(x)极小值=f=--+1.命题点 3 已知极值求参数例 3 (1)已知 f(x)=x3+3ax2+bx+a2在 x=-1 时有极值 0,则 a-b=________.(2)若函数 f(x)=-x2+x+1 在区间(,3)上有极值点,则实数 a 的取值范围是____________.答案 (1)-7 (2)(2,)解析 (1)由题意得 f′(x)=3x2+6ax+b,则解得或经检验当 a=1,b=3 时,函数 f(x)在 x=-1 处无法取得极值,1而 a=2,b=9 满足题意,故 a-b=-7.(2)若函数 f(x)在区间(,3)上无极值,则当 x∈(,3)时,f′(x)=x2-ax+1≥0 恒成立或当 x∈(,3)时,f′(x)=x2-ax+1≤0 恒成立.当 x∈(,3)时,y=x+的值域是[2,);当 x∈(,3)时,f′(x)=x2-ax+1≥0,即 a≤x+恒成立,a≤2;当 x∈(,3)时,f′(x)=x2-ax+1≤0,即 a≥x+恒成立,a≥.因此要使函数 f(x)在(,3)上有极值点,实数 a 的取值范围是(2,).思维升华 (1)求函数 f(x)极值的步骤:① 确定函数的定...