圆周运动知识点及例题eVIP免费

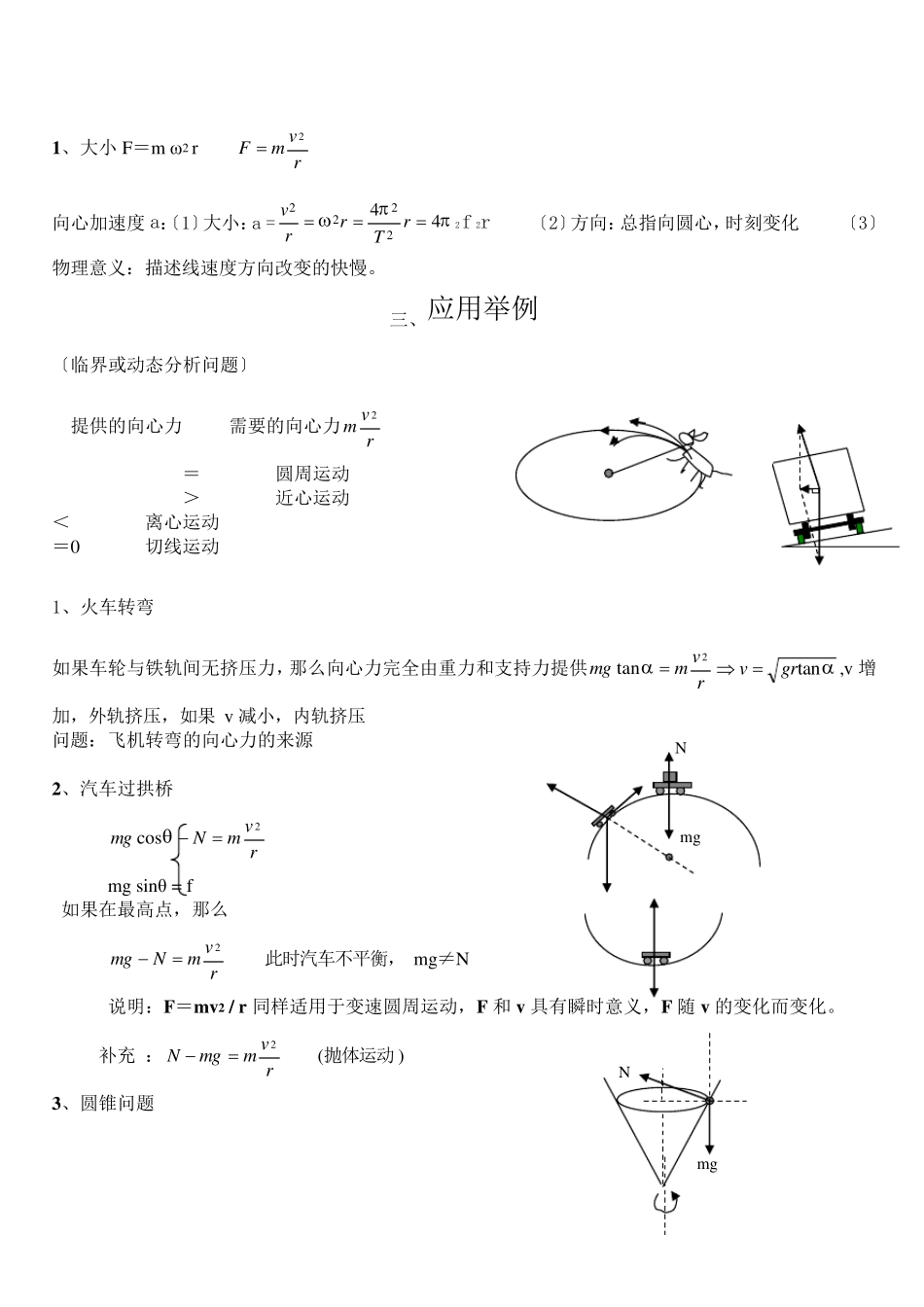
匀速圆周运动知识点及例题 二、匀速圆周运动的描述 1．线速度、角速度、周期和频率的概念 (1) 线速度v 是描述质点沿圆周运动快慢的物理量，是矢量，其大小为Trtsv2; 其方向沿轨迹切线，国际单位制中单位符号是m/s； 〔2〕角速度ω是描述质点绕圆心转动快慢的物理量，是矢量，其大小为Tt2； 在国际单位制中单位符号是rad／s； (3〕周期T 是质点沿圆周运动一周所用时间，在国际单位制中单位符号是s； 〔4〕频率f 是质点在单位时间内完成一个完整圆运动的次数，在国际单位制中单位符号是 Hz； 〔5〕转速n 是质点在单位时间内转过的圈数，单位符号为r／s，以及r／min． 2、速度、角速度、周期和频率之间的关系 线速度、角速度、周期和频率各量从不同角度描述质点运动的快慢，它们之间有关系v＝rω．fT1，Tv2，f2。 由上可知，在角速度一定时，线速度大小与半径成正比；在线速度一定时，角速度大小与半径成反比． 三、向心力和向心加速度 1．向心力 〔1〕向心力是改变物体运动方向，产生向心加速度的原因． 〔2〕向心力的方向指向圆心，总与物体运动方向垂直，所以向心力只改变速度的方向． 2．向心加速度 〔1〕向心加速度由向心力产生，描述线速度方向变化的快慢，是矢量． 〔2〕向心加速度方向与向心力方向恒一致，总沿半径指向圆心；向心加速度的大小为 22224Trrrvan 公式： 1.线速度V＝s/t＝2πr/T 2.角速度ω＝Φ/t＝2π/T＝2πf 3.向心加速度a＝V2/r＝ω2r＝(2π/T)2r 4.向心力F心＝mV2/r＝mω2r＝mr(2π/T)2＝mωv=F合 5.周期与频率：T＝1/f 6.角速度与线速度的关系：V＝ωr 7.角速度与转速的关系ω＝2πn(此处频率与转速意义相同) 8.主要物理量及单位：弧长s:米(m)；角度Φ：弧度〔rad〕；频率f：赫〔Hz〕；周期T：秒〔s〕；转速n：r/s；半径r：米〔m〕；线速度V：〔m/s〕；角速度ω：〔rad/s〕；向心加速度：〔m/s2〕。 二、向心力和加速度 1、大小F＝m ω2 r rvmF2 向心加速度a：〔1〕大小：a =442222rTrrv2 f 2r 〔2〕方向：总指向圆心，时刻变化 〔3〕物理意义：描述线速度方向改变的快慢。 三、应用举例 〔临界或动态分析问题〕 提供的向心力 需要的向心力rvm2 ＝ 圆周运动 ＞ 近心运动 ＜ 离心运动 ＝0 切线运动 1、火车转弯 如果车轮与铁轨间无挤压力，那么向心力完全由重力和支持力提供rvmmg2tantangrv ,...