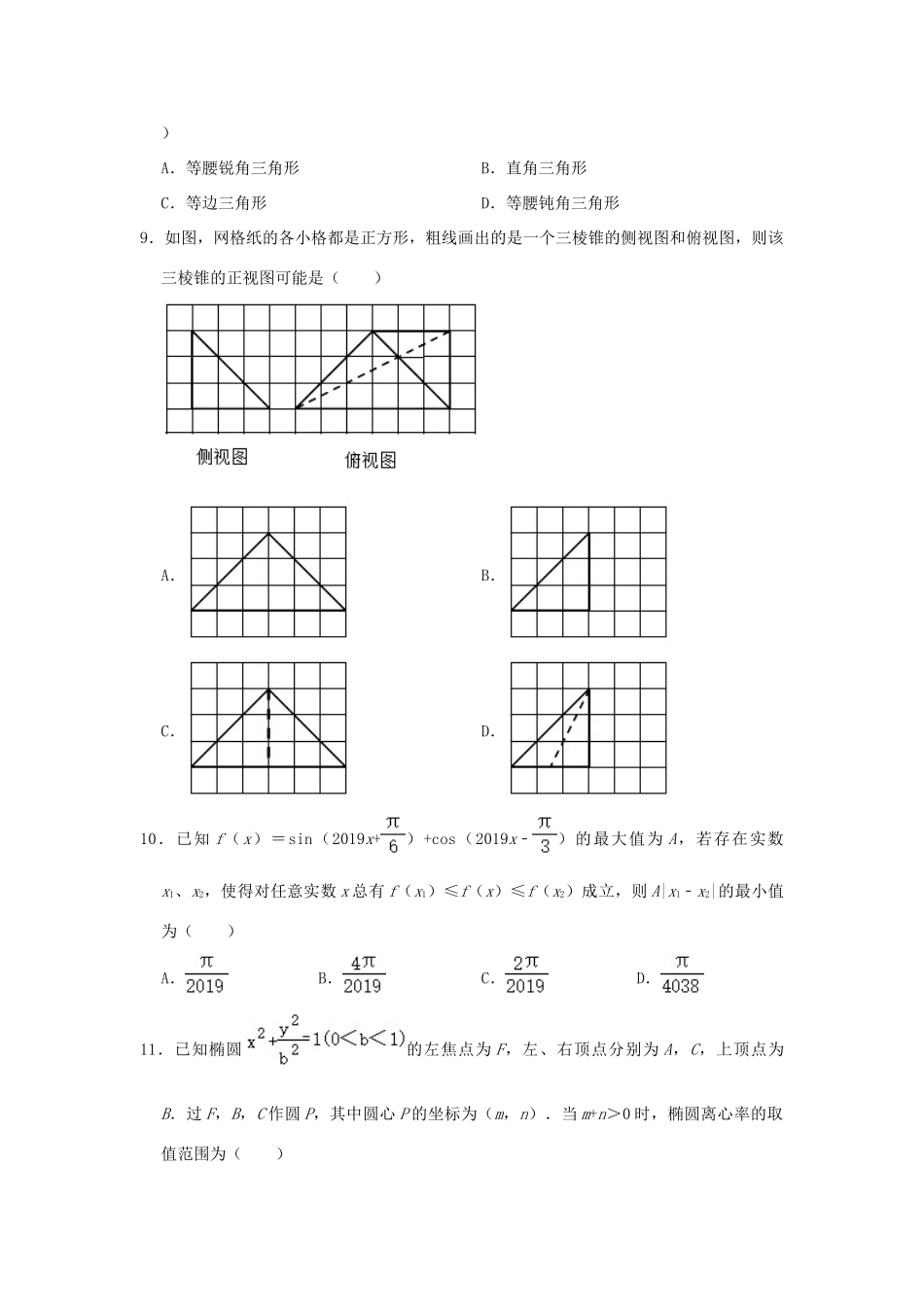
河北省衡水中学 2020 届高三数学上学期四调考试试题 文(含解析)一、选择题(本大题共 12 小题,每题 5 分,共 60 分,下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)1.设集合 M={﹣1,2,3},N={a+2,a2+2},且 M∩N={3},则实数 a 的值为( )A.1 或﹣1B.﹣1C.1D.22.AB 是抛物线 y2=2x 的一条焦点弦,|AB|=4,则 AB 中点 C 的横坐标是( )A.2B.C.D.3.已知{an}是等比数列,且 an>0,a2a4+2a3a5+a4a6=25,那么 a3+a5的值等于( )A.5B.10C.15D.204.与双曲线有共同的渐近线,且经过点 A(﹣3,)的双曲线的一个焦点到一条渐近线的距离是( )A.8B.4C.2D.15.△ABC 是边长为 2 的等边三角形,已知向量 , 满足=2 ,=2 + ,则下列结论正确的是( )A.| |=1B. ⊥C. • =1D.(4 + )⊥6.存在函数 f(x)满足,对任意 x∈R 都有( )A.f(sin2x)=sinxB.f(sin2x)=x2+xC.f(x2+1)=|x+1|D.f(x2+2x)=|x+1|7.已知双﹣y2=1(a>0)的左、右焦点分别曲线为 F1,F2,离心率为,P 为双曲线右支上一点,且满足|PF1|2﹣|PF2|2=4,则△PF1F2的周长为( )A.2B.2+2C.2+4D.2+48 . 已 知 函 数 f ( x ) 为 R 上 的 可 导 函 数 , 其 导 函 数 为 f' ( x ) , 且 f ( x ) =,在△ABC 中,f(A)=f'(B)=1,则△ABC 的形状为( )A.等腰锐角三角形B.直角三角形C.等边三角形D.等腰钝角三角形9.如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )A.B.C.D.10.已知 f(x)=sin(2019x+)+cos(2019x﹣)的最大值为 A,若存在实数x1、x2,使得对任意实数 x 总有 f(x1)≤f(x)≤f(x2)成立,则 A|x1﹣x2|的最小值为( )A.B.C.D.11.已知椭圆的左焦点为 F,左、右顶点分别为 A,C,上顶点为B.过 F,B,C 作圆 P,其中圆心 P 的坐标为(m,n).当 m+n>0 时,椭圆离心率的取值范围为( )A.B.C.D.12.设 D=+a+2.其中 e≈2.71828,则 D 的最小值为( )A.B.C.+1D.+1二、填空题(本大题共 4 小题,每题 5 分,共 20 分)13.南北朝时,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究做出了一定的贡献.例如算经中有一道题为:“今有...