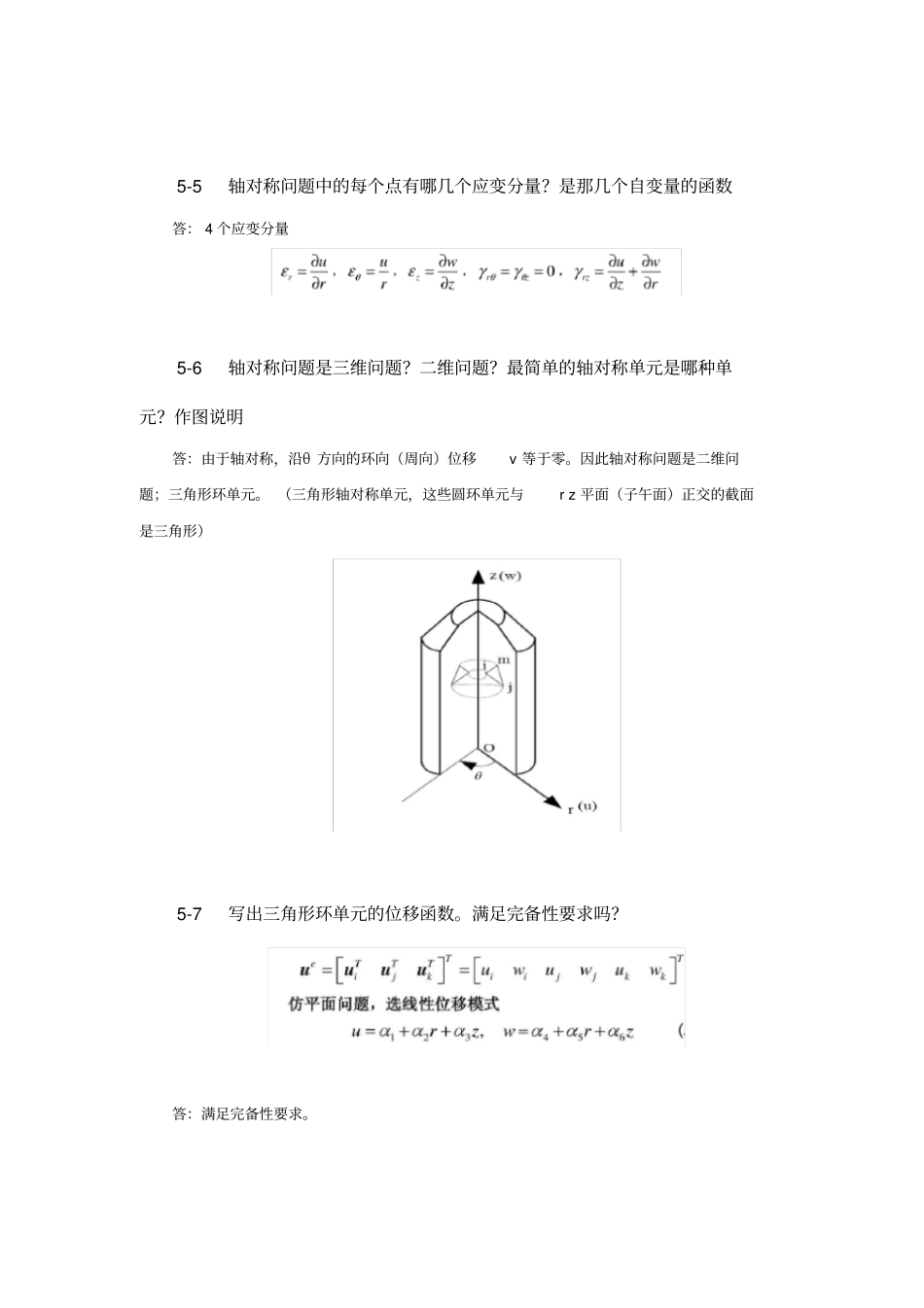
思考题5-1 轴对称问题的定义答:工程中又一类结构,其几何形状、边界条件、所受载荷都对称于某一轴线,这种情况下结构再载荷作用下位移、应变和应力也对称于这个轴线,这种问题成为轴对称问题。5-2 轴对称问题一般采用的坐标系?作图说明每个坐标分量的物理意义答:在描述轴对称弹性体问题的应力及变形时常采用圆柱坐标r,θ ,z。5-3 轴对称问题中每个点有几个位移分量?各位移分量是那几个自变量的函数?答:位移分量u, w,都只是 rz 的函数,与θ 无关。5-4 轴对称问题中的每个点有哪几个应力分量?是那几个自变量的函数。答: 4 个应力分量;5-5 轴对称问题中的每个点有哪几个应变分量?是那几个自变量的函数答: 4 个应变分量5-6 轴对称问题是三维问题?二维问题?最简单的轴对称单元是哪种单元?作图说明答:由于轴对称,沿θ 方向的环向(周向)位移v 等于零。因此轴对称问题是二维问题;三角形环单元。 (三角形轴对称单元,这些圆环单元与r z 平面(子午面)正交的截面是三角形)5-7 写出三角形环单元的位移函数。满足完备性要求吗?答:满足完备性要求。5-8 三角形环单元形函数的表达式?指出形函数的性质。5-9 三角形环单元的应力和应变的特点。其单元刚度矩阵是几阶的?答:应力分量:剪应力为常量,其他3 个正应力分量均随位置变化;应变分量:面内(子五面)3 个应变分量为常量,环向应变不是常应变,而是与单元中各点的位置有关。单元刚度矩阵为六阶。5-10 有限元方法求解对称问题的基本步骤?1.结构离散化:对整个结构进行离散化,将其分割成若干个单元,单元间彼此通过节点相连;2. 求出各单元的刚度矩阵[K](e) :[K](e) 是由单元节点位移量{ Φ }(e)求单元节点力向量{F}(e)的转移矩阵,其关系式为:{F}(e)= [K](e) {Φ }(e);3. 集成总体刚度矩阵[K]并写出总体平衡方程:总体刚度矩阵[K] 是由整体节点位移向量{ Φ }求整体节点力向量的转移矩阵,其关系式为{F}= [K] {Φ },此即为总体平衡方程。4. 引入支撑条件,求出各节点的位移:节点的支撑条件有两种:一种是节点n 沿某个方向的位移为零,另一种是节点n 沿某个方向的位移为一给定值。5. 求出各单元内的应力和应变对于有限元方法,其基本思路和解题步骤可归纳为:(1) 建立积分方程,根据变分原理或方程余量与权函数正交化原理,建立与微分方程初边值问题等价的积分表达式,这是有限元法的出发点。(2) 区域单元剖分,根据求解区域...