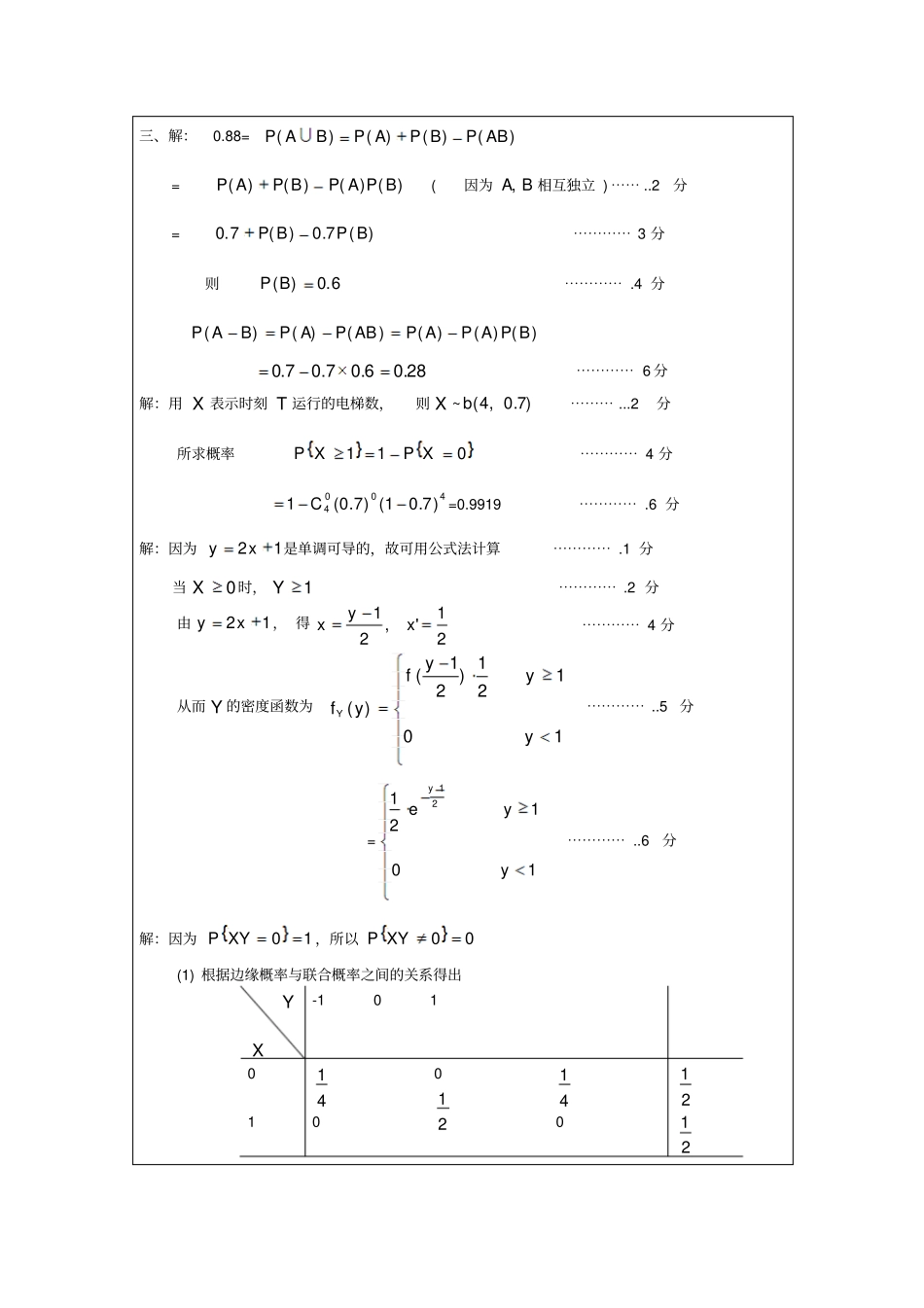
一、单项选择题( 每题 3 分 共 18 分) (1).0)(,0)(;;0)(0)();(( ).,0)(ABPAP(D)BA(C)BPAP(B)BA(A)ABPBA则同时出现是不可能事件与或互不相容互斥与则以下说法正确的是适合、若事件(2)设随机变量X 其概率分布为 X -1 0 1 2 P 0.2 0.3 0.1 0.4 则}5.1{ XP()。(A)0.6 (B) 1 (C) 0 (D) 21设事件1A 与2A 同时发生必导致事件A 发生,则下列结论正确的是()(A))()(21AAPAP(B)1)()()(21APAPAP(C))()(21AAPAP(D)1)()()(21APAPAP).54,0);46,0();3,0();5,0(~,72,),1,2(~),1,3(~(D)N(C)N(B)N(A)ZYXZYXNYNX则令相互独与且设随机变量(N立).(1.D 2 . A 3 .B 4 .A 5 .A 6 .B 填空题 1.)(BP2. 000)(xxxexfx, (1)如果)()(,0)(,0)(APBAPBPAP,则)(ABP(2)设随机变量 X 的分布函数为.0,)1(1,0,0)(xexxxFx则 X 的密度函数)(xf,)2( XP . 三、 (6 分) 设BA,相互独立,7.0)(AP,88.0)(BAP,求)(BAP.四、(6 分)某宾馆大楼有4 部电梯,通过调查,知道在某时刻T,各电梯在运行的概率均为0.7 ,求在此时刻至少有1 台电梯在运行的概率。五、(6 分)设随机变量X 的概率密度为其它,00,)(xexfx,求随机变量Y=2X+1的概率密度。六、(8 分) 已知随机变量X 和 Y 的概率分布为X101Y10P412141P2121(1) 而且1}0{ XYP. 求随机变量 X 和 Y 的联合分布 ; (2)判断 X 与 Y 是否相互独立? 七、(8 分)设二维随机变量),(YX的联合密度函数为.,0,0,0,12),()43(其他yxeyxfyx求:(1))20,10(YXP;(2)求 X 的边缘密度。八、(6 分)一工厂生产的某种设备的寿命(以年计)服从参数为的指数分布。工厂规定,出售的设备在售出一年之内损坏可予以调换。若工厂售出一台设备盈利100 元,调换一台设备厂方需花费300 元,求工厂出售一台设备净盈利的期望。十、(7 分)设供电站供应某地区1 000 户居民用电,各户用电情况相互独立。已知每户每日用电量(单位:度)服从[0 ,20] 上的均匀分布,利用中心极限定理求这1 000 户居民每日用电量超过10 100 度的概率。(所求概率用标准正态分布函数)(x 的值表示)三、解: 0.88=)()()()(ABPBPAPBAP =)()()()(BPAPBPAP (因为BA,相互独立 ) ⋯⋯ ..2分 =)(7.0)(7.0BPBP⋯⋯⋯⋯ 3 分则6.0)(BP⋯⋯⋯⋯ .4 分)()()()()()(BPAPAPABPAPBAP28.06.07.07.0⋯⋯⋯⋯ 6 分解:用 X 表示时刻 T 运行的电梯数,则 X ~)7.0,4...