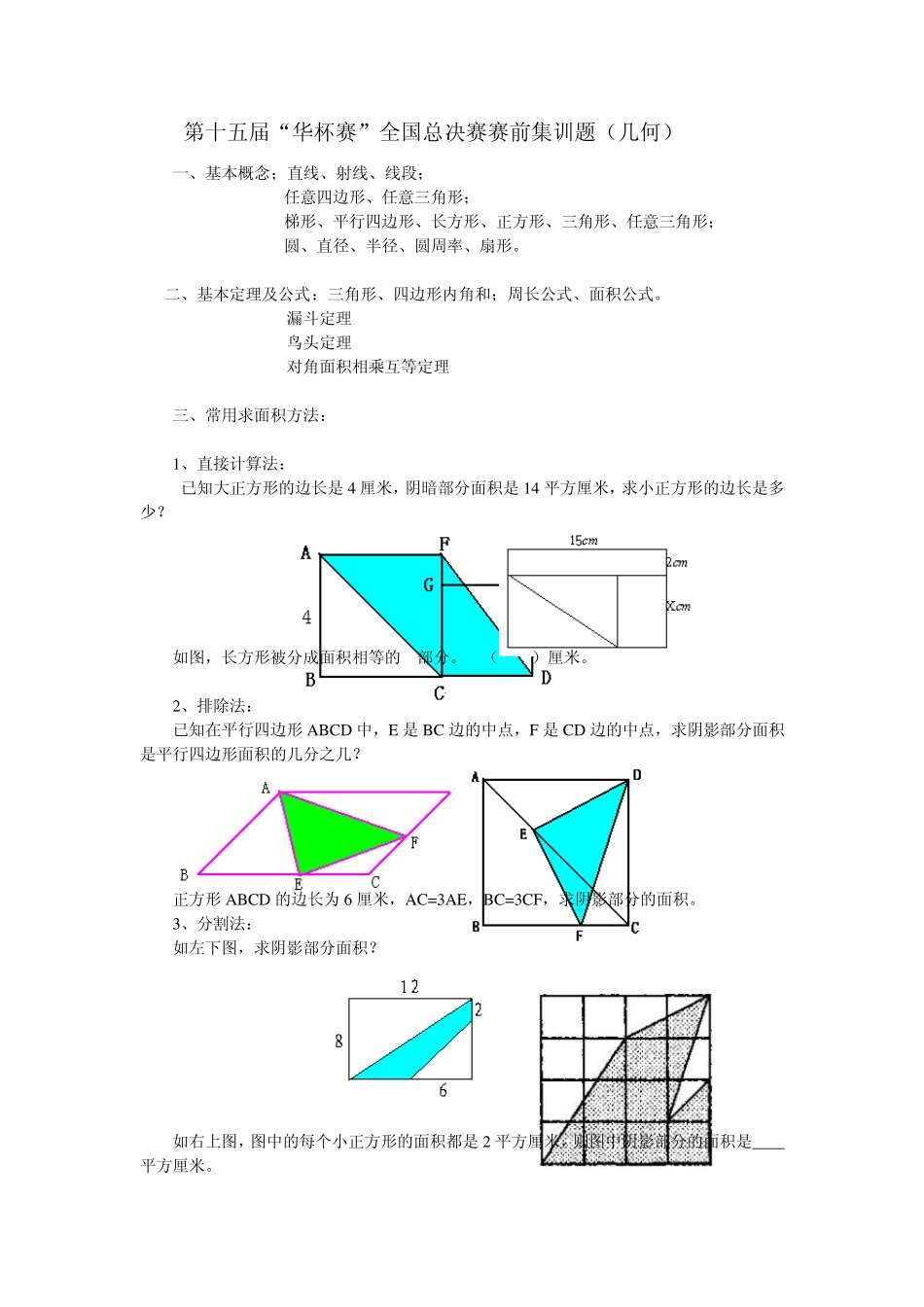
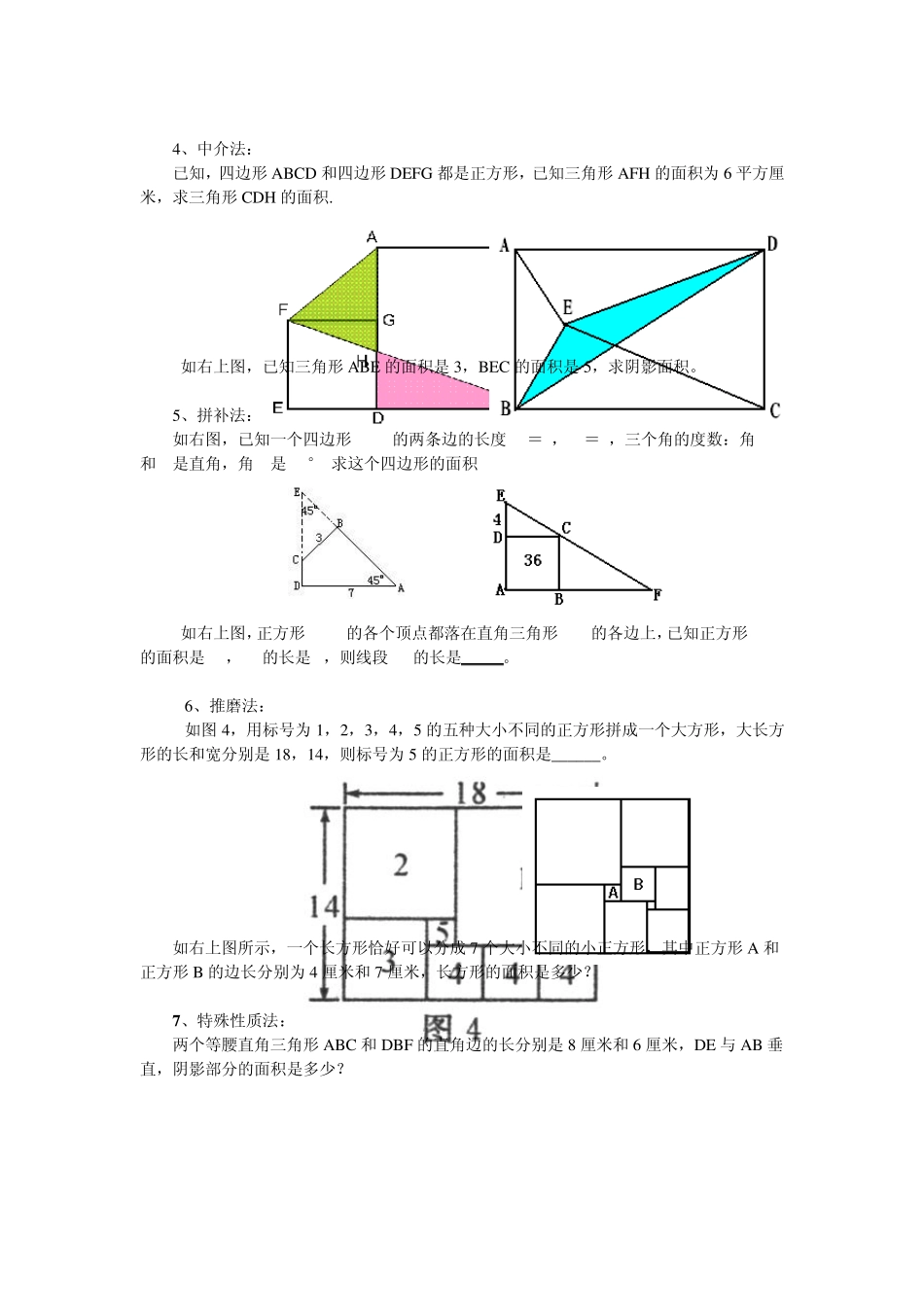
第十五届“华杯赛”全国总决赛赛前集训题(几何) 一、基本概念;直线、射线、线段; 任意四边形、任意三角形; 梯形、平行四边形、长方形、正方形、三角形、任意三角形; 圆、直径、半径、圆周率、扇形。 二、基本定理及公式:三角形、四边形内角和;周长公式、面积公式。 漏斗定理 鸟头定理 对角面积相乘互等定理 三、常用求面积方法: 1、直接计算法: 已知大正方形的边长是 4 厘米,阴暗部分面积是 14 平方厘米,求小正方形的边长是多少? 如图,长方形被分成面积相等的 4部分。X=( )厘米。 2、排除法: 已知在平行四边形 ABCD 中,E 是 BC 边的中点,F 是 CD 边的中点,求阴影部分面积是平行四边形面积的几分之几? 正方形 ABCD 的边长为 6 厘米,AC=3AE,BC=3CF,求阴影部分的面积。 3、分割法: 如左下图,求阴影部分面积? 如右上图,图中的每个小正方形的面积都是 2 平方厘米,则图中阴影部分的面积是____平方厘米。 4、中介法: 已知,四边形ABCD 和四边形DEFG 都是正方形,已知三角形AFH 的面积为6 平方厘米,求三角形CDH 的面积. 如右上图,已知三角形ABE 的面积是3,BEC 的面积是5,求阴影面积。 5、拼补法: 如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角 B和D是直角,角A是45°.求这个四边形的面积. 如右上图,正方形ABCD的各个顶点都落在直角三角形AEF的各边上,已知正方形ABCD的面积是36,DE的长是4,则线段 BF的长是 。 6、推磨法: 如图4,用标号为1,2,3,4,5 的五种大小不同的正方形拼成一个大方形,大长方形的长和宽分别是18,14,则标号为5 的正方形的面积是______。 如右上图所示,一个长方形恰好可以分成 7 个大小不同的小正方形,其中正方形A 和正方形B 的边长分别为4 厘米和7 厘米,长方形的面积是多少? 7 、特殊性质法: 两个等腰直角三角形ABC 和DBF 的直角边的长分别是8 厘米和6 厘米,DE 与 AB 垂直,阴影部分的面积是多少? 右上图是一块正方形的地板砖示意图,各部分相互对称,红色小正方形的面积是4,四块绿色小三角形的面积总和是18,求大正方形ABCD的面积。 8、旋转法: 左下图,等腰直角三角形ABC 和四分之一圆DEB,AB=5 厘米,BE=2 厘米,求图中阴影部分的面积。 在三角形ABC 中,∠ABC=90 度,AC =8 厘米,BC=6 厘米,分别以AC、BC 为边作正方形AEDC、BCFG ,则三角形BEF 的...