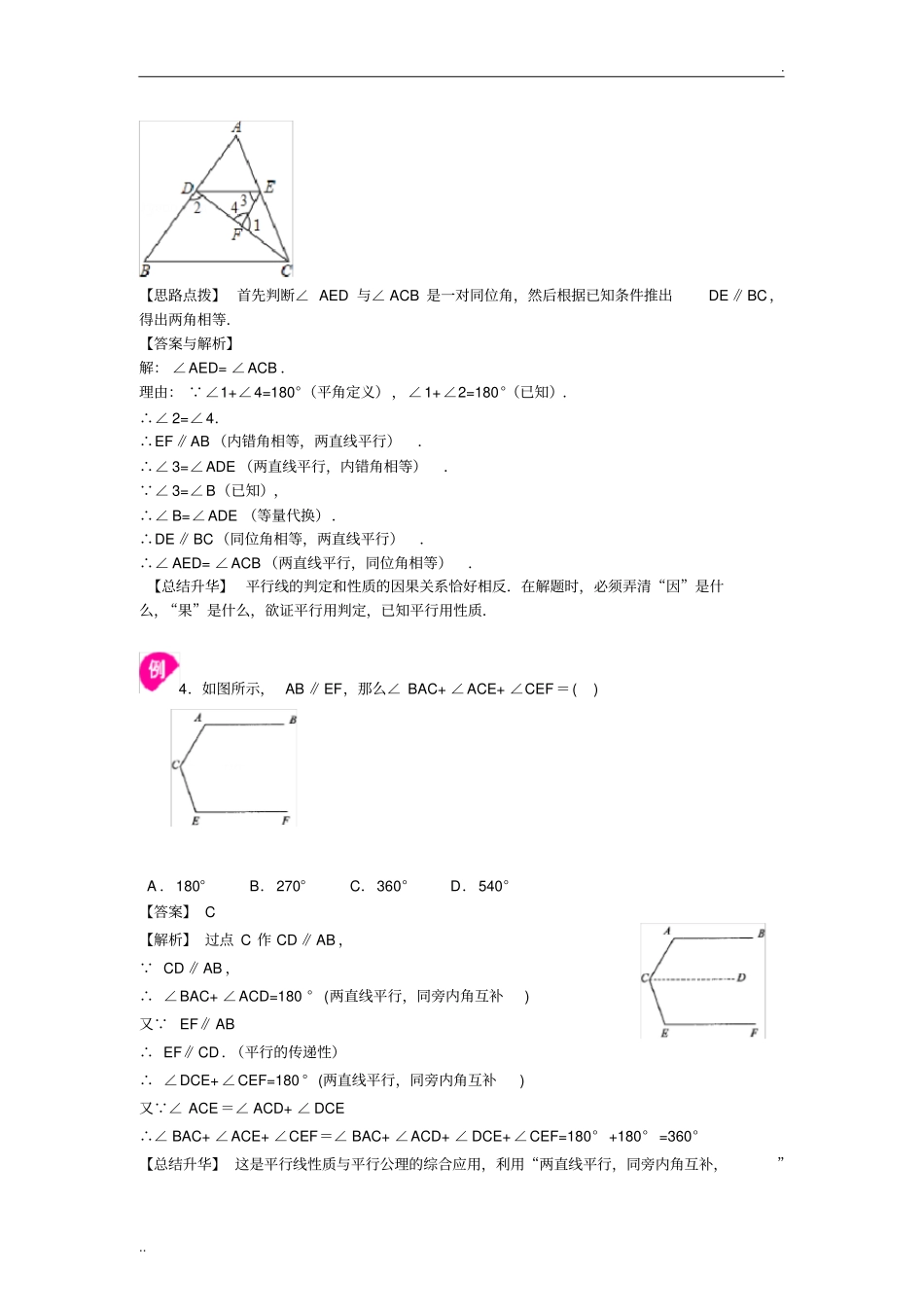
. .. 平行线的性质(基础)知识讲解【学习目标】1.掌握平行线的性质,并能依据平行线的性质进行简单的推理;2.了解平行线的判定与性质的区别和联系,理解两条平行线的距离的概念;【要点梳理】要点一、平行线的性质性质 1:两直线平行,同位角相等;性质 2:两直线平行,内错角相等;性质 3:两直线平行,同旁内角互补.要点诠释:(1)“同位角相等、内错角相等”、“同旁内角互补”都是平行线的性质的一部分内容,切不可忽视前提“两直线平行” .( 2) 从角的关系得到两直线平行,是平行线的判定; 从平行线得到角相等或互补关系,是平行线的性质.要点二、平行的传递性如果两条直线都与第三条直线平行,那么这两条直线也互相平行.要点三、两条平行线的距离同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.要点诠释:(1)求两条平行线的距离的方法是在一条直线上任找一点,向另一条直线作垂线,垂线段的长度就是两条平行线的距离.( 2) 两条平行线的位置确定后,它们的距离就是个定值,不随垂线段的位置的改变而改变,即平行线间的距离处处相等.【典型例题】类型一、平行线的性质1.如图所示,如果AB ∥DF, DE∥BC ,且∠ 1=65° .那么你能说出∠2、∠ 3、∠ 4的度数吗 ?为什么.【思路点拨】 本题已知条件中,包含了两个层次:第一层次是由DE∥BC ,可得∠ 1=∠ 4,∠1+∠2= 180° ;第二层次是由DF∥AB ,可得∠ 3=∠ 2 或∠ 3+∠4=180° ,从而解出∠ 2、∠3、∠ 4 的度数.【答案与解析】. .. 解: DE ∥BC,∴∠4=∠ 1=65° ( 两直线平行,内错角相等) .∠2+∠1=180° ( 两直线平行,同旁内角互补) .∴∠2=180° - ∠1=180° - 65° = 115° .又 DF∥ AB ( 已知 ) ,∴∠3=∠ 2(两直线平行,同位角相等) .∴∠3=115°( 等量代换 ) .【总结升华】 平行线的性质:由两条直线平行的位置关系得到两个相关角的数量关系.举一反三:【变式】(2015?大连)如图, AB ∥CD ,∠A=56 °,∠C=27°,则 ∠ E 的度数为.【答案】 29° .解: AB ∥CD ,∴∠ DFE=∠A=56 °,又 ∠C=27°,∴∠ E=56°﹣27°=29°. 类型二、两平行线间的距离2.如图所示,直线l1∥l 2,点 A、B 在直线 l2 上,点 C、 D 在直线 l1 上,若△ ABC 的面积为 S1,△ ABD 的面积为 S2,则 () A.S1>S...