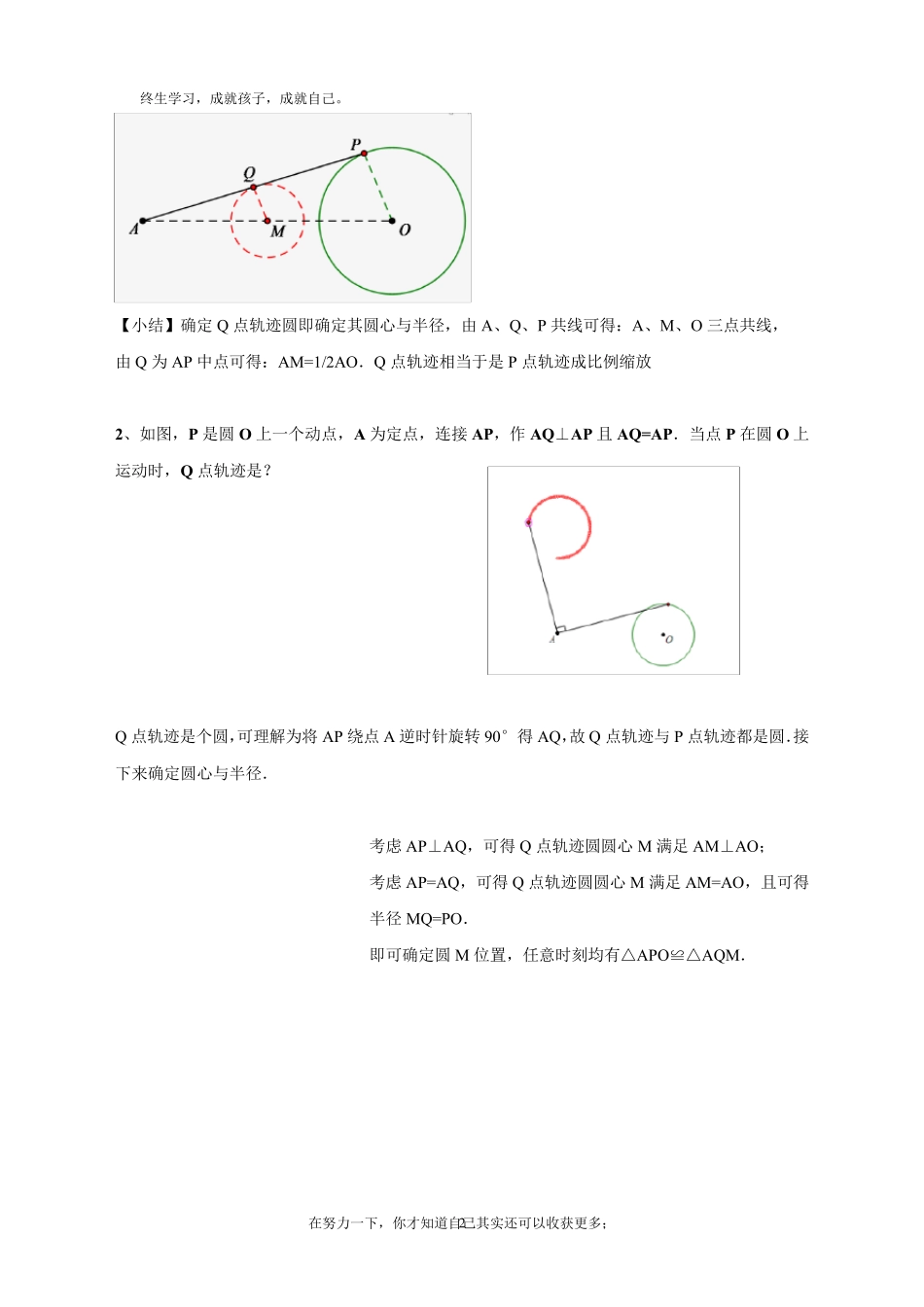
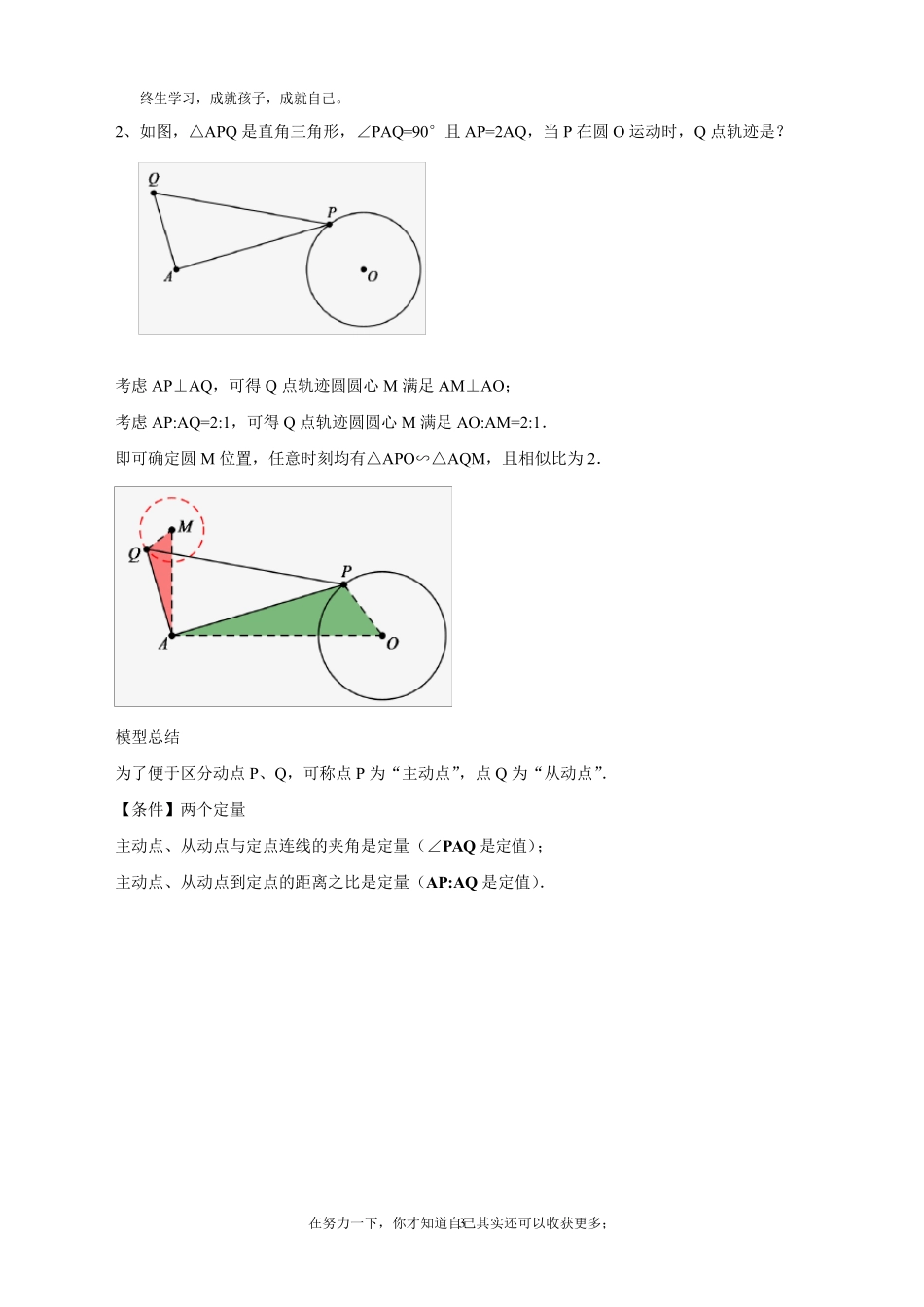
终生学习,成就孩子,成就自己。 在努力一下,你才知道自己其实还可以收获更多; 1 教师姓名 杨老师 学生姓名 年级 初三 上课时间 学科 数学 课题名称 轨迹问题解决方法之瓜豆原理 教学目标 1、掌握圆形轨迹最值问题 2、掌握直线型轨迹最值问题 3、掌握瓜豆原理勾画轨迹的问题 轨迹问题解决方法之瓜豆原理 【知识要点】 在辅助圆问题中,我们了解了求关于动点最值问题的方式之一——求出动点轨迹,即可求出关于动点的最值.所以寻找到动点的轨迹,然后在计算,是一种不错的解决最值问题的方法。 本文讨论另一类动点引发的最值问题,在此类题目中,题目或许先描述的是动点P,但最终问题问的可以是另一点Q,当然 P、Q 之间存在某种联系,从P 点出发探讨 Q 点运动轨迹并求出最值,为常规思路 【例题精讲】 知识点一、轨迹是圆 1、如图,P 是圆O 上一个动点,A 为定点,连接AP,Q 为AP 中点.当点P 在圆O 上运动时,Q 点轨迹是? 点Q 轨迹是个圆,而我们还需确定的是此圆与圆O 有什么关系? 考虑到 Q 点始终为AP 中点,连接AO,取AO 中点M,则M 点即为Q 点轨迹圆圆心,半 径 MQ是 OP 一半 ,任 意 时刻 ,均 有△ AMQ ∽ △ AOP,Q M:PO=AQ :AP=1:2. 终生学习,成就孩子,成就自己。 在努力一下,你才知道自己其实还可以收获更多; 2 【小结】确定Q 点轨迹圆即确定其圆心与半径,由A、Q 、P 共线可得:A、M、O 三点共线, 由Q 为AP 中点可得:AM=1/2AO.Q 点轨迹相当于是P 点轨迹成比例缩放 2、如图,P 是圆O 上一个动点,A 为定点,连接AP,作AQ ⊥AP 且AQ =AP.当点P 在圆O 上运动时,Q 点轨迹是? Q 点轨迹是个圆,可理解为将AP 绕点A 逆时针旋转90°得AQ ,故 Q 点轨迹与P 点轨迹都是圆.接下来确定圆心与半径. 考虑 AP⊥AQ ,可得Q 点轨迹圆圆心M 满足 AM⊥AO; 考虑 AP=AQ ,可得Q 点轨迹圆圆心M 满足 AM=AO,且可得 半径MQ =PO. 即可确定圆M 位置,任意时刻均有△APO≌△AQ M. 终生学习,成就孩子,成就自己。 在努力一下,你才知道自己其实还可以收获更多; 3 2 、如图,△APQ 是直角三角形,∠PAQ=90°且 AP=2AQ ,当 P 在圆 O 运动时,Q 点轨迹是? 考虑 AP⊥AQ ,可得 Q 点轨迹圆圆心 M 满足 AM⊥AO; 考虑 AP:AQ =2:1,可得 Q 点轨迹圆圆心 M 满足 AO:AM=2:1. 即可确定圆 M 位置,任...