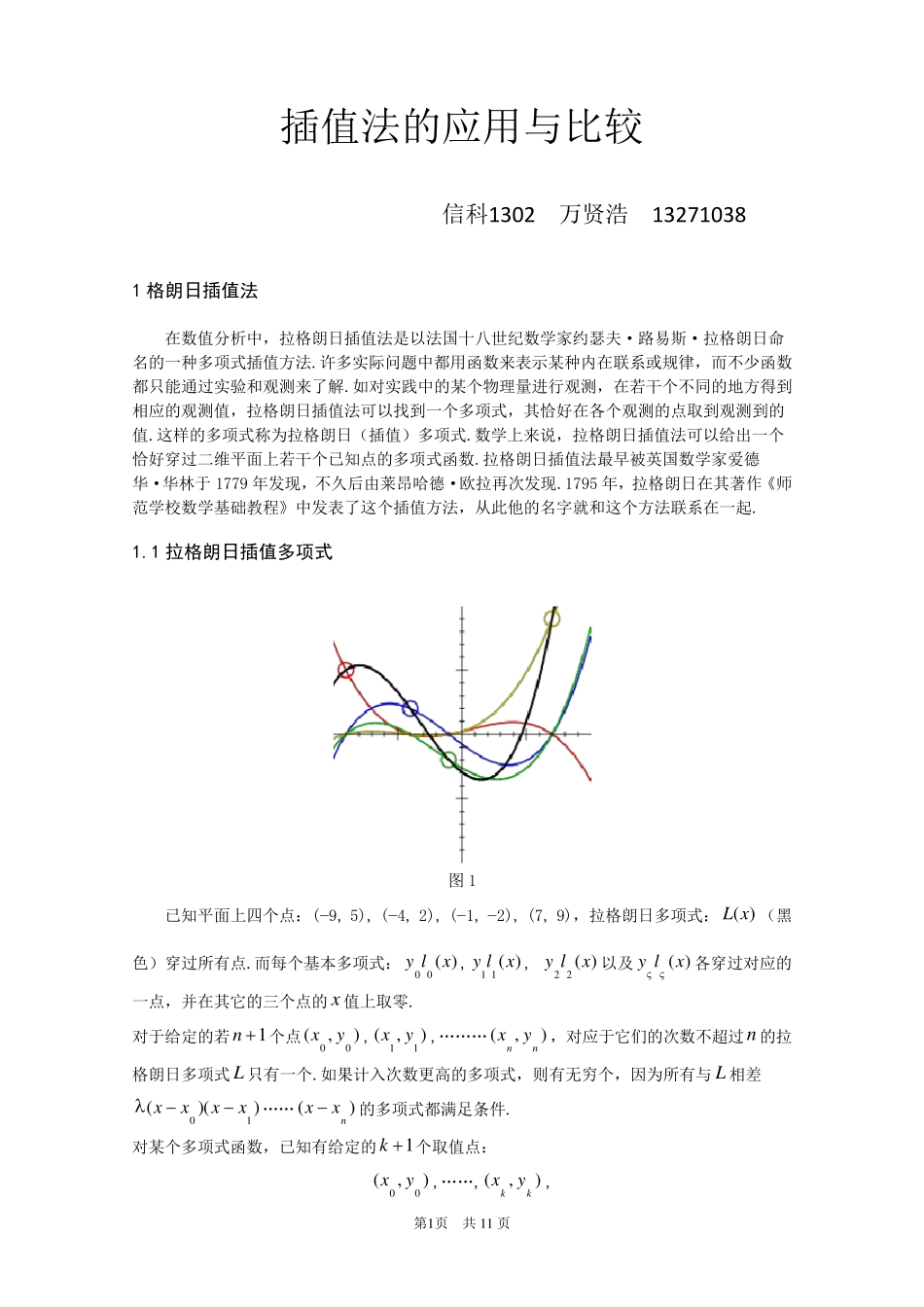
第1 页 共1 1 页 插值法的应用与比较 信科1302 万贤浩 13271038 1 格朗日插值法 在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法.许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解.如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值.这样的多项式称为拉格朗日(插值)多项式.数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数.拉格朗日插值法最早被英国数学家爱德华·华林于1779 年发现,不久后由莱昂哈德·欧拉再次发现.1795 年,拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法,从此他的名字就和这个方法联系在一起. 1.1 拉格朗日插值多项式 图 1 已知平面上四 个点: (−9, 5), (−4, 2), (−1, −2), (7, 9),拉格朗日多项式:)(xL(黑色 )穿过所 有 点.而每 个基本 多项式:)(00xly,)(11xly, )(22xly以及)(xly各穿过对应的一点,并 在其它 的三 个点的x值上取零 . 对于给定 的若1n个点),(00 yx,),(11 yx,… … …),(nn yx,对应于它 们 的次数不超 过n 的拉格朗日多项式 L 只有 一个.如果 计 入 次数更 高 的多项式,则 有 无 穷 个,因 为所 有 与L 相差))((10xxxx… …)(nxx 的多项式都满 足 条 件 . 对某个多项式函数,已知有 给定 的1k个取值点: ),(00 yx,… … ,),(kk yx, 第2 页 共1 1 页 其中ix 对应着自变量的位置,而iy 对应着函数在这个位置的取值. 假设任意两个不同的ix 都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为: )()(0xlyxLjkjj, 其中每个)(xlj为拉格朗日基本多项式(或称插值基函数),其表达式为: )()()()()()()()()(111100,0kjkjjjjjjjkjiiijijxxxxxxxxxxxxxxxxxxxxxl, 拉格朗日基本多项式 xli的特点是在jx 上取值为1,在其它的点ix ,ji 上取值为0 . 例:设有某个多项式函数f ,已知它在三个点上的取值为: • 1 0)4(f, • 2 5.5)5(f, • 1)6(f, 要求)1 8(f的值. 首先写出每个拉格朗日基本多项式: )64)(54()6)(5(0xxxl;...