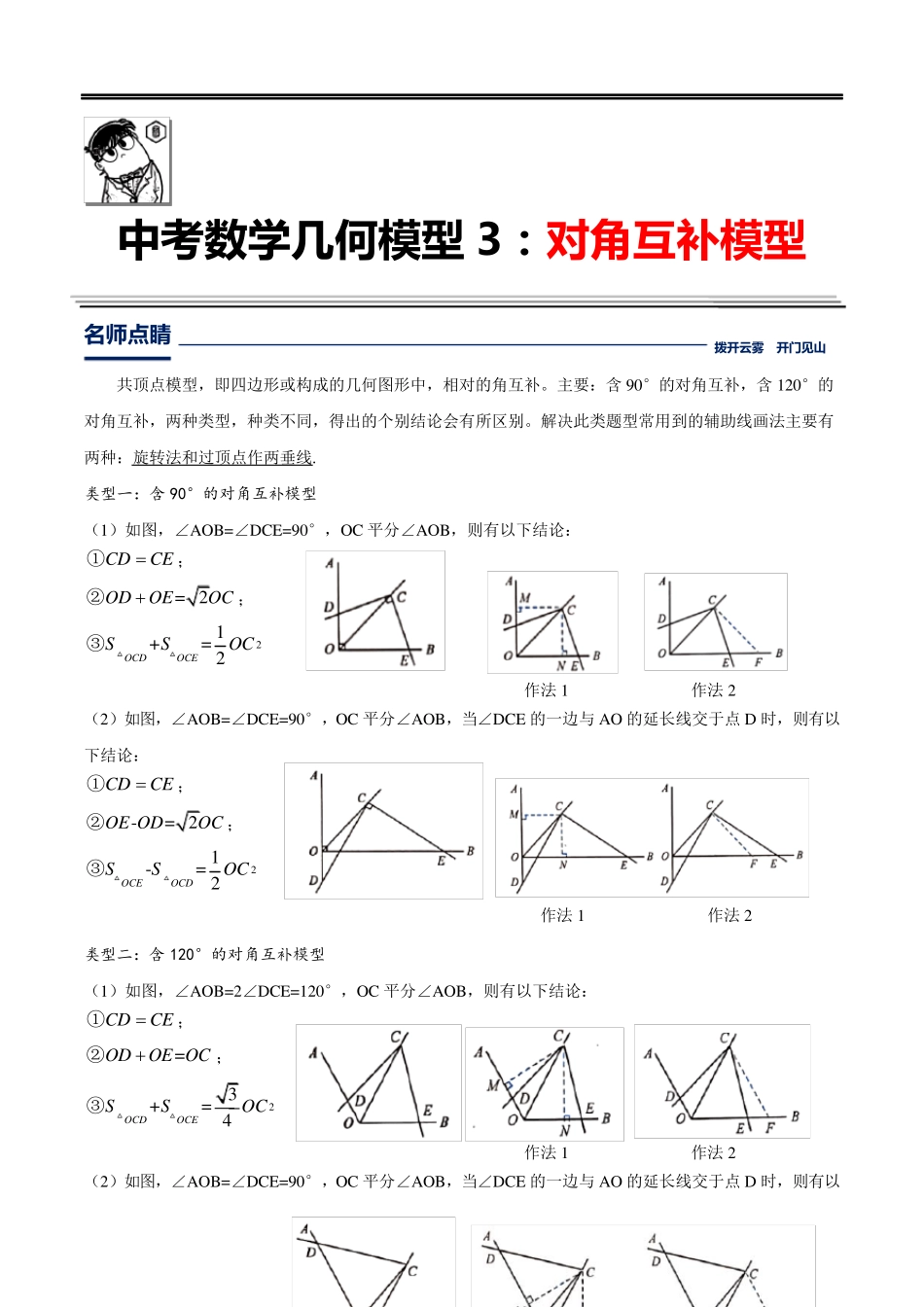
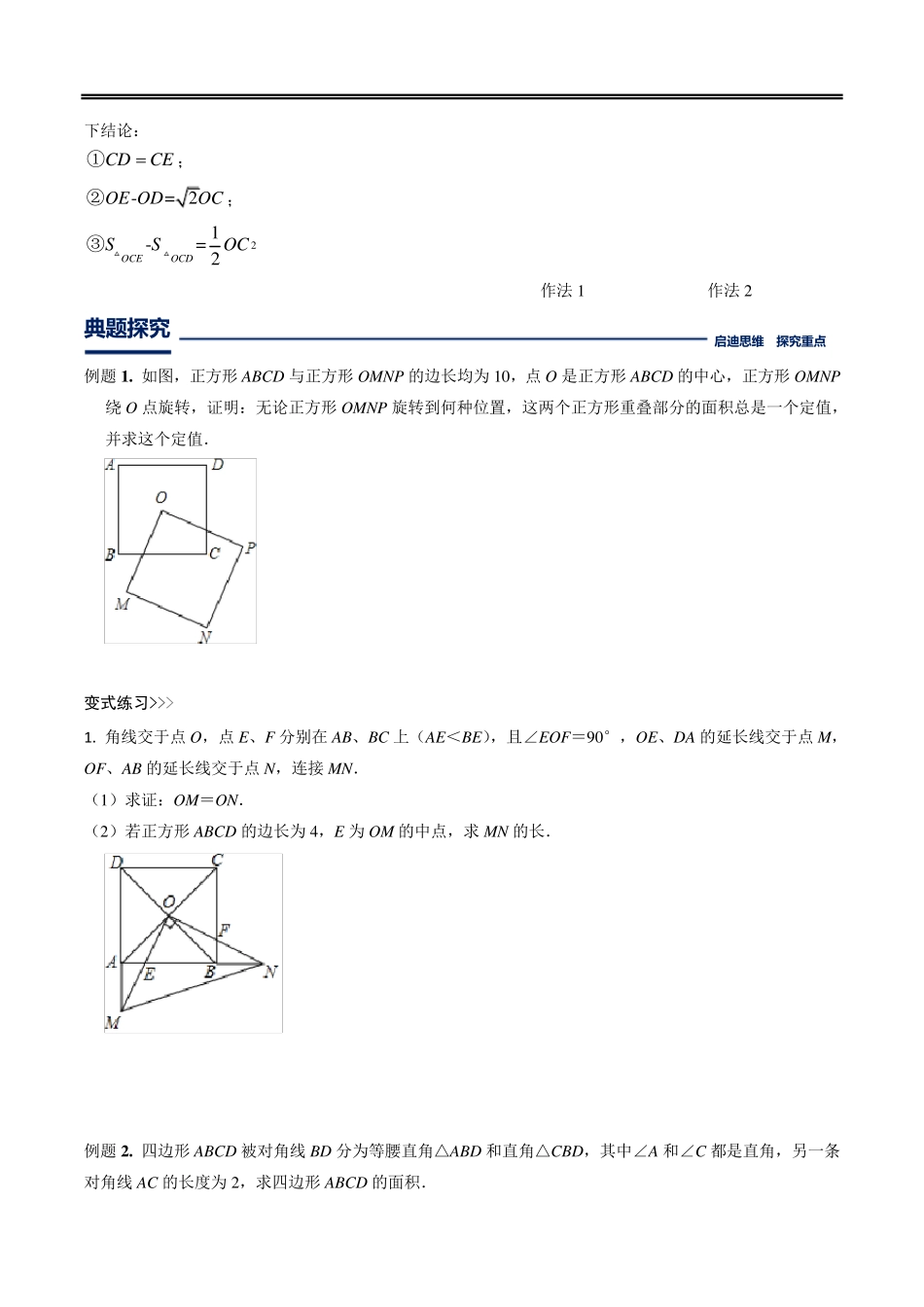
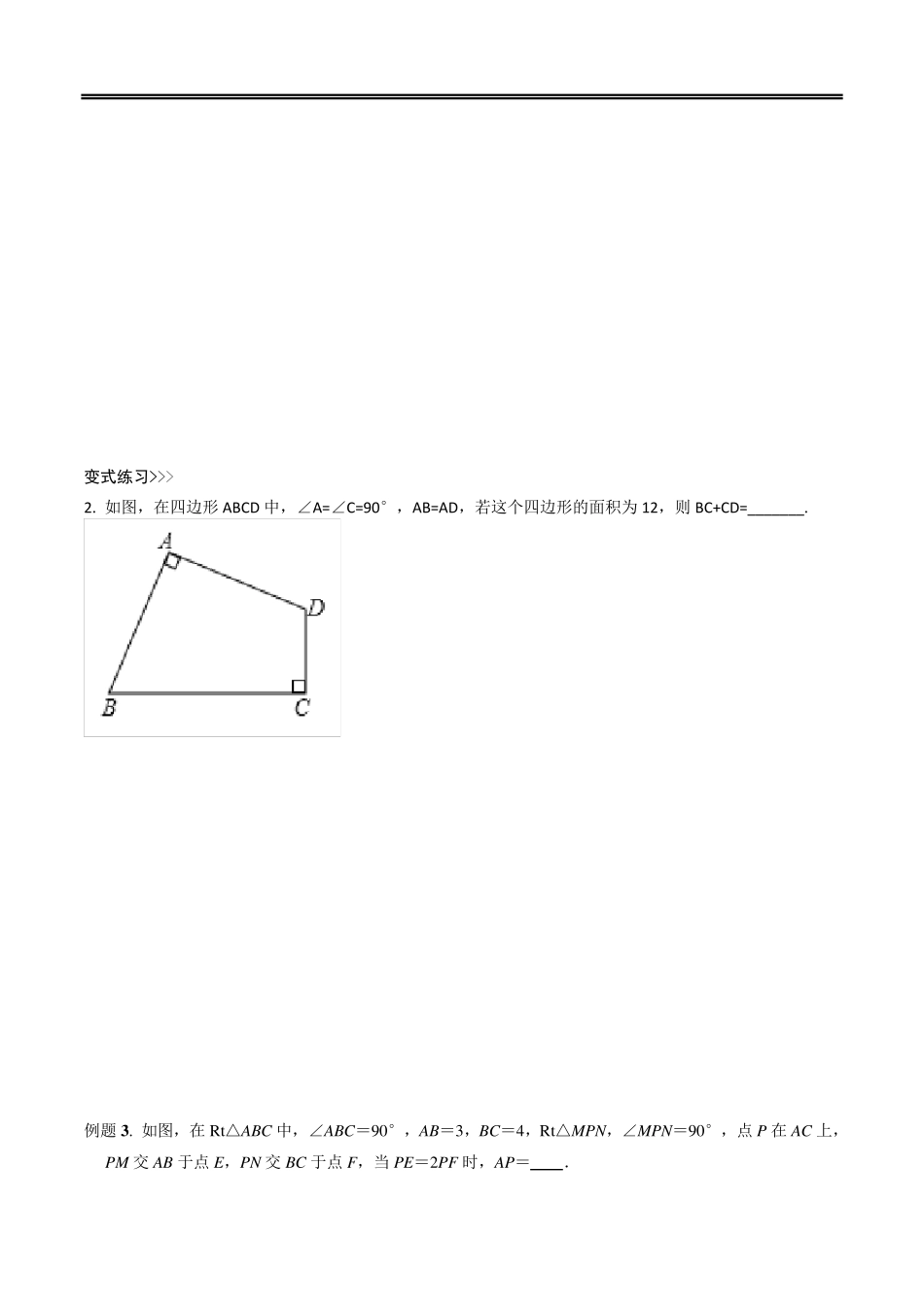
中考 数 学 几 何 模 型 3: 对 角 互 补 模 型 名 师 点 睛 拨 开 云 雾 开 门 见 山 共顶点模型,即四边形或构成的几何图形中,相对的角互补。主要:含90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线. 类型一:含90°的对角互补模型 (1)如图,∠AOB=∠DCE=90°,OC 平分∠AOB,则有以下结论: CDCE①; = 2ODOEOC②; 21+= 2OCDOCESSOC③ 作法1 作法2 (2)如图,∠AOB=∠DCE=90°,OC 平分∠AOB,当∠DCE 的一边与AO 的延长线交于点D 时,则有以下结论: CDCE①; -= 2OE ODOC②; 21-= 2OCEOCDSSOC③ 作法1 作法2 类型二:含120°的对角互补模型 (1)如图,∠AOB=2∠DCE=120°,OC 平分∠AOB,则有以下结论: CDCE①; =ODOE OC②; 23+= 4OCDOCESSOC③ 作法1 作法2 (2)如图,∠AOB=∠DCE=90°,OC 平分∠AOB,当∠DCE 的一边与AO 的延长线交于点D 时,则有以 下结论: CDCE①; -= 2OE ODOC②; 21-= 2OCEOCDSSOC③ 作法1 作法2 典题 探 究 启 迪 思 维 探 究 重 点 例题1. 如图,正方形ABCD 与正方形OMNP 的边长均为10,点O 是正方形ABCD 的中心,正方形OMNP绕O 点旋转,证明:无论正方形OMNP 旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值. 变式练习>>> 1. 角线交于点O,点E、F 分别在AB、BC 上(AE<BE),且∠EOF=90°,OE、DA 的延长线交于点M, OF、AB 的延长线交于点N,连接MN. (1)求证:OM=ON. (2)若正方形ABCD 的边长为4,E 为OM 的中点,求MN 的长. 例题2. 四边形ABCD 被对角线BD 分为等腰直角△ABD 和直角△CBD,其中∠A 和∠C 都是直角,另一条 对角线AC 的长度为2,求四边形ABCD 的面积. 变式练习>>> 2. 如图,在四边形ABCD 中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD=_______. 例题3. 如图,在Rt△ABC 中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P 在AC 上,PM 交AB 于点E,PN 交BC 于点F,当PE=2PF 时,AP= . 变式练习>>> 3. 如图,在矩形ABCD 中,AB=3,BC=5,点E 在对角线AC 上,连接BE,作EF⊥BE,垂足为E,直线EF 交线段DC 于点F,则=( ) A. B. C. D. 例题...