数理方程练习题VIP免费

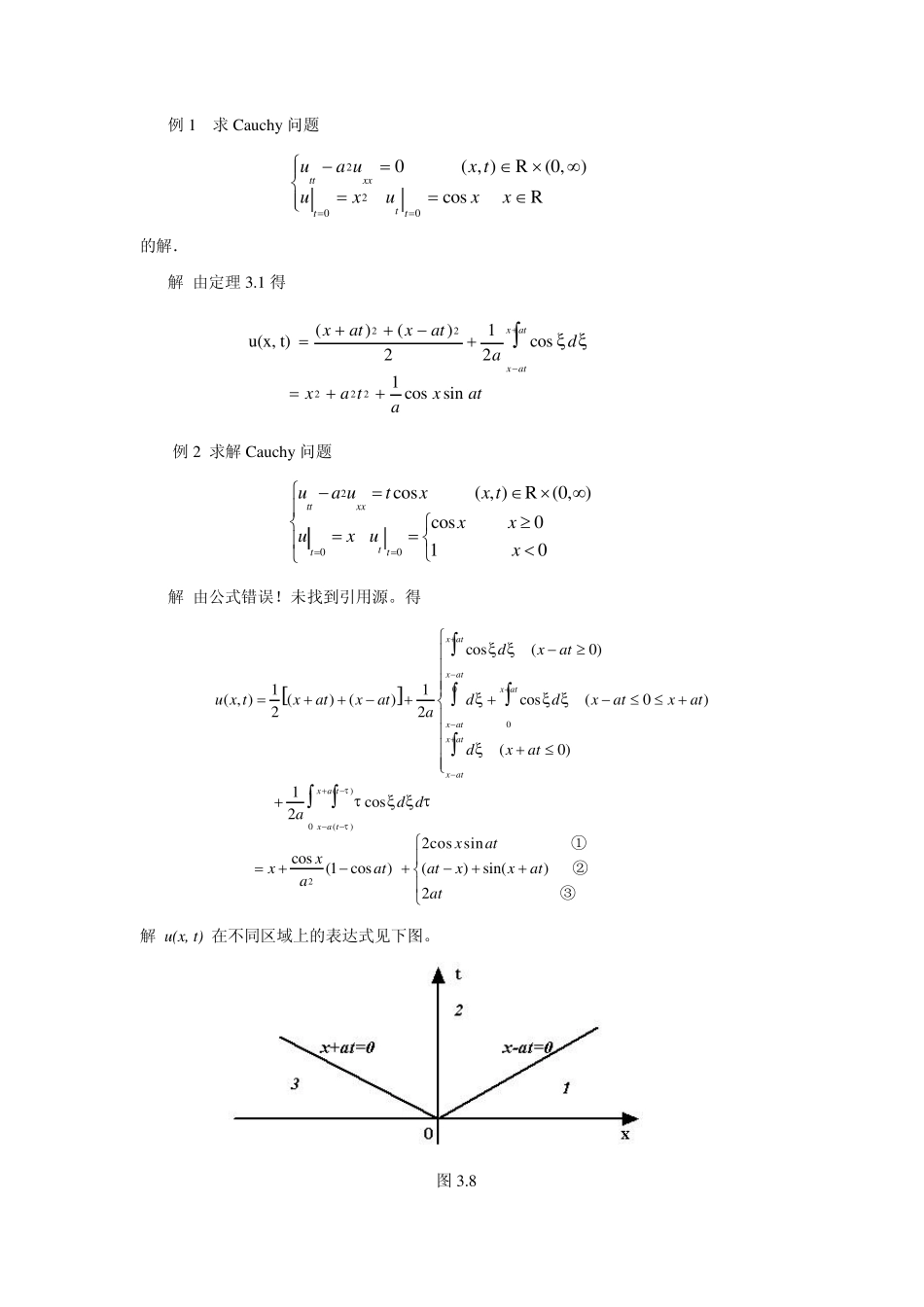
数理方程练习题一（2009 研） 1. 设( , )uu x y，求二阶线性方程 20ux y  的一般解。 解 先把所给方程改写为 ()0uxy 2分 两边对 x积分，得 ()0( )( )uu dxdxyyyxy 4分 这里， ( )y是任意函数。再两边对 y 积分，得方程的一般解为 y ( )( )( )( )uudyy dyf xf xg yy 6分 这里，( ), ( )f x g y 是任意两个一次可微函数。 2. 设 22()ufxy 满足 Laplace 方程 22220uuxy 求函数u. 解: 22 ,,.rxryrxyxrxr ''( ),( ).uxuyfrfrxryr 3分 因此有 222'''223222'''223( )( )( )( )uxyfrfrxrruyxfrfryrr 3分 原方程化为: '''1( )( )0frfrr 2分 故有:221212( )lnlnxyruf rcccc 2分 例1 求Cau chy 问题 22000( , )(0,)costtxxtttua ux tuxuxxRR 的解． 解 由定理3.1 得 22222()()1u (x , t)cos221 cossinx atx atxatxatdaxa txata  例2 求解Cau chy 问题 200cos( , )(0, )cos010ttxxtttua utxx txxux ux R 解 由公式错误！未找到引用源。得 00()0()2cos(0)11( , )()()cos(0)22(0)1cos22cos sincos(1cos)()sin()2x atx atx atx atx atx atx a ttx a tdxatu x txatxatddxatxatadxatd daxatxxatatxxataat     ①②③ 解 u(x, t) 在不同区域上的表达式见下图。 图 3.8 例3 解在半无界问题 20000( , )(0, )sin(0)0(0)ttxxtttxua ux tux uxxut R 解 易知定理3.5 的条件满足，从而 ()()1sin()22( , )()()1sin()22sin sinsin sinsin sinx atx atx atat xxatxatdxatau x txatatxdxataxxatxatxxatxatxxat      例1 求解二维Cauchy 问题 2222000( , , )(0,)0()( , )tttttuaux y tuuxxyx y RR 解 由...