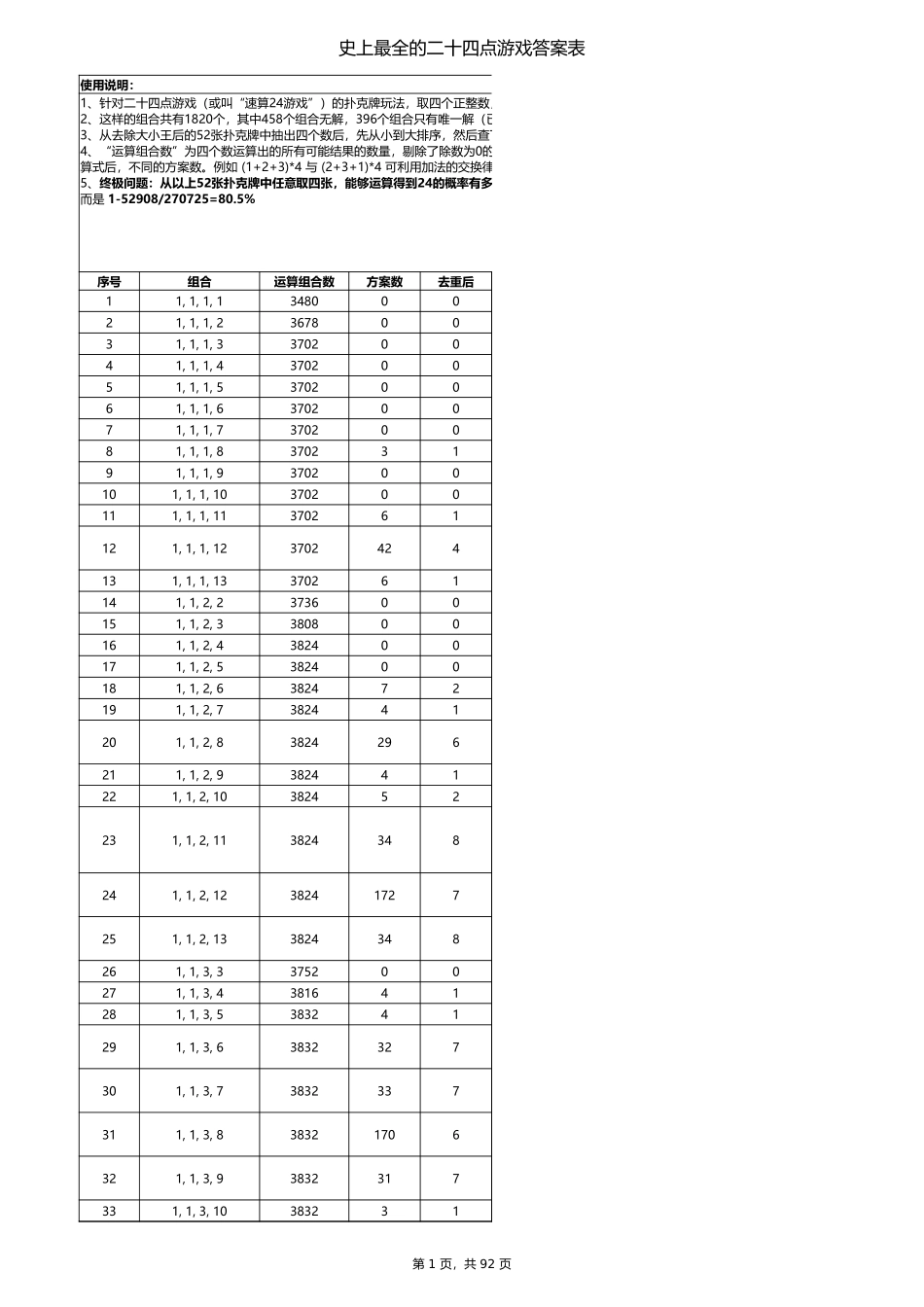
史上最全的二十四点游戏答案表第 1 页,共 92 页使用说明:序号组合运算组合数方案数去重后11, 1, 1, 134800021, 1, 1, 236780031, 1, 1, 337020041, 1, 1, 437020051, 1, 1, 537020061, 1, 1, 637020071, 1, 1, 737020081, 1, 1, 837023191, 1, 1, 9370200101, 1, 1, 10370200111, 1, 1, 11370261121, 1, 1, 123702424131, 1, 1, 13370261141, 1, 2, 2373600151, 1, 2, 3380800161, 1, 2, 4382400171, 1, 2, 5382400181, 1, 2, 6382472191, 1, 2, 7382441201, 1, 2, 83824296211, 1, 2, 9382441221, 1, 2, 10382452231, 1, 2, 113824348241, 1, 2, 1238241727251, 1, 2, 133824348261, 1, 3, 3375200271, 1, 3, 4381641281, 1, 3, 5383241291, 1, 3, 63832327301, 1, 3, 73832337311, 1, 3, 838321706321, 1, 3, 93832317331, 1, 3, 103832311、针对二十四点游戏(或叫“速算24游戏”)的扑克牌玩法,取四个正整数,范围介于1~13之间,计算所有组合通过加、减、乘、除和括号运算得到24的方案数。2、这样的组合共有1820个,其中458个组合无解,396个组合只有唯一解(已剔除重复),读者可利用下表筛选鉴别;3、从去除大小王后的52张扑克牌中抽出四个数后,先从小到大排序,然后查下表,可得答案。例如:(8,5,12,3)的组合,查 (3,5,8,12);4、“运算组合数”为四个数运算出的所有可能结果的数量,剔除了除数为0的情况,最大为3888;“方案数”为运算结果=24的数量,“去重后”为剔除了本质上相同的运算式后,不同的方案数。例如 (1+2+3)*4 与 (2+3+1)*4 可利用加法的交换律变为同一种形式,本质上是相同的,所以有必要剔除重复的结果。5、终极问题:从以上52张扑克牌中任意取四张,能够运算得到24的概率有多大?因为以下1820种组合的每一种出现的可能性不同,所以答案不是 1-458/1820=74.8%,而是 1-52908/270725=80.5%史上最全的二十四点游戏答案表第 2 页,共 92 页序号组合运算组合数方案数去重后341, 1, 3, 11383241351, 1, 3, 123832296361, 1, 3, 13383282371, 1, 4, 4375261381, 1, 4, 53816317391, 1, 4, 638321706401, 1, 4, 73832337411, 1, 4, 83832348421, 1, 4, 9383282431, 1, 4, 10383211441, 1, 4, 11383200451, 1, 4, 12383292461, 1, 4, 13383200471, 1, 5, 5375...