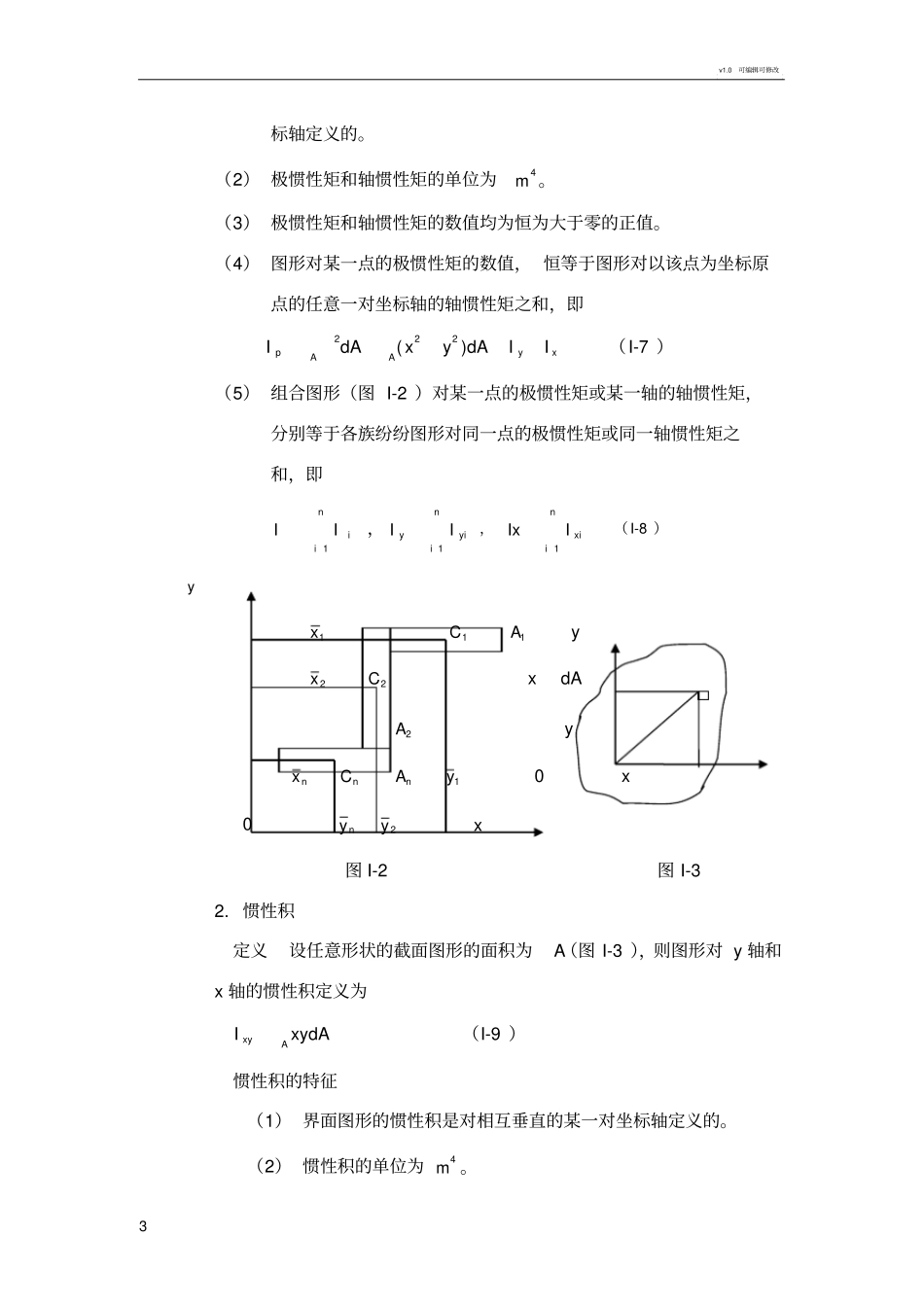
v1.0 可编辑可修改1 惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一. 重点及难点:( 一). 截面静矩和形心1. 静矩的定义式如图 1 所示任意有限平面图形,取其单元如面积dA ,定义它对任意轴的一次矩为它对该轴的静矩,即 yydAdSxxdAdSy x dA整个图形对 y、z 轴的静矩分别为x×C y AAyydASxxdAS(I-1 ) 0 A y x2. 形心与静矩关系图 I-1 设平面图形形心C的坐标为CC zy ,则 0 ASyx,ASxy(I-2 )推论 1 如果 y 轴通过形心(即0x),则静矩0yS;同理,如果 x 轴通过形心(即0y),则静矩0Sx;反之也成立。推论 2 如果 x、y 轴均为图形的对称轴,则其交点即为图形形心;如果y 轴为图形对称轴,则图形形心必在此轴上。3. 组合图形的静矩和形心设截面图形由几个面积分别为nAAAA321,,的简单图形组成, 且一直各族图形的形心坐标分别为332211,,,yxyxyx;;,则图形对 y 轴和 x 轴的静矩分别为v1.0 可编辑可修改2 niniiixixniiiniyiyyASSxAS1111S(I-3 )截面图形的形心坐标为niiniiiAxAx11,niiniiiAyAy11(I-4 )4. 静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。(2) 静矩有的单位为3m 。(3) 静矩的数值可正可负,也可为零。图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零, 则该轴必通过图形的形心。(4) 若已知图形的形心坐标。则可由式(I-1 )求图形对坐标轴的静矩。若已知图形对坐标轴的静矩,则可由式(I-2 )求图形的形心坐标。组合图形的形心位置,通常是先由式(I-3 )求出图形对某一坐标系的静矩,然后由式( I-4 )求出其形心坐标。(二) . 惯性矩 惯性积 惯性半径1. 惯性矩定义 设任意形状的截面图形的面积为A(图 I-3 ),则图形对 O点的极惯性矩定义为ApdAI2(I-5 )图形对 y 轴和 x 轴的光性矩分别定义为AydAxI2,dAyIAx2(I-6 )惯性矩的特征(1) 界面图形的极惯性矩是对某一极点定义的;轴惯性矩是对某一坐v1.0 可编辑可修改3 标轴定义的。(2) 极惯性矩和轴惯性矩的单位为4m 。(3) 极惯性矩和轴惯性矩的数值均为恒为大于零的正值。(4) 图形对某一点的极惯性矩的数值, 恒等于图形对以该点为坐标原点的任意一对坐标轴的轴惯性矩之和,即AxyApIIdAyxdAI)(222(I-7 )(5) 组合图形(图 I-2 )对某一点的极惯性矩或某一轴的轴惯性矩,分别等于各族纷纷图形对同一点的极惯...