初三相似三角形的基本模型VIP免费

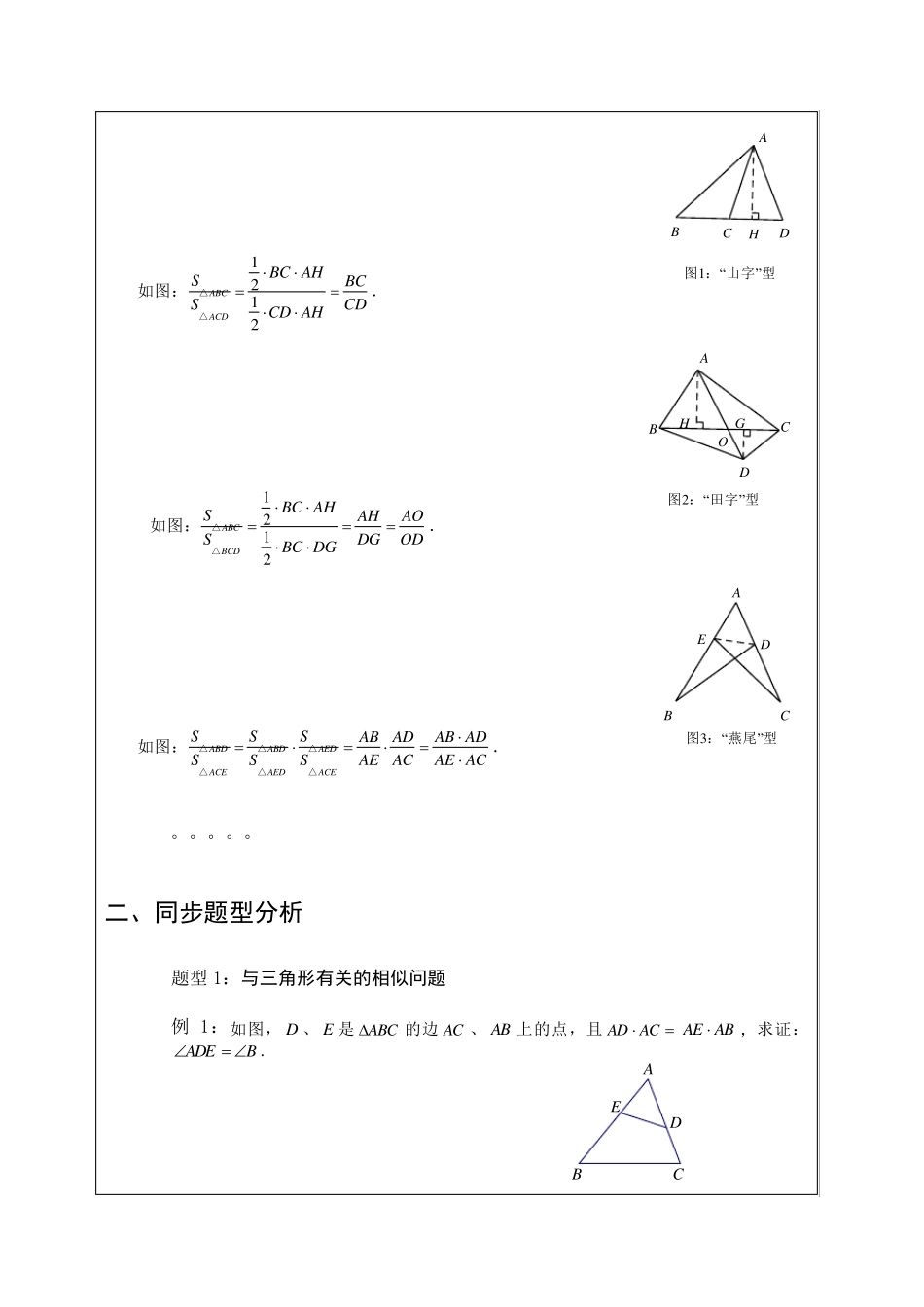
相似三角形 一、同步知识梳理 知识点 1：相似证明中的基本模型 IHGFEDCBAGFEDCBAEDCBAEDCBA EFDCBAFEDCBAODCBAODCBA HEDCBAEDCBAEDCBAODCBA DCBDBACAEDCBADCBA GFEDCBAGFEDCBAGFEDCBADEFCBA HPMNFEDCBAGHGFEDCBAEFDCBAFEDCBA 知识点2：相似证明中常见辅助线的作法 在相似的证明中，常见的辅助线的作法是做平行线构造成比例线段或相似三角形，同时再结合等量代换得到要证明的结论．常见的等量代换包括等线代换、等比代换、等积代换等． 如图：AD 平分BAC交BC 于D ，求证：BDABDCAC． 321EDCAB 证法一：过C 作CEAD∥，交BA 的延长线于E ． ∴1E ，23  ． 12  ，∴3E ．∴ACAE． ADCE∥，∴BDBABADCBEAC． 点评：做平行线构造成比例线段，利用了“A”型图的基本模型． BACDE12 证法二；过B 作AC 的平行线，交AD 的延长线于E ． ∴12E  ，∴ABBE． BEAC∥，∴BDBEABDCACAC． 点评：做平行线构造成比例线段，利用了“X”型图的基本模型． 知识点3：相似证明中的面积法 面积法主要是将面积的比，和线段的比进行相互转化来解决问题． 常用的面积法基本模型如下： 图1 ：“山字”型HDCBA 如图：1212ABCACDBC AHSBCSCDCD AH△△． 图2 ：“田字”型GHODCBA 如图：1212ABCBCDBC AHSAHAOSDGODBC DG△△． 图3 ：“燕尾”型CDEBA 如图：ABDABDAEDACEAEDACESSSABADAB ADSSSAEACAE AC△△△△△△． 。。。。。 二、同步题型分析 题型1：与三角形有关的相似问题 例 1：如图， D 、 E 是ABC的边 AC 、 AB 上的点，且 AD AC AE AB，求证：ADEB . BAEDC DCBA 解析： 例2：如图，在ABC中，ADBC于 D ，CEAB于 E，ABC的面积是BDE面积 的 4 倍，6AC ，求 DE 的长. 解析： 题型 2：相似中的角平分线问题 例1：如图，AD 是 ABC的角平分线，求证：ABBDACCD 解析： 例2：已知ABC中，BAC的外角平分线交对边 BC 的延长线于 D ，求证：ABBDACCD 解析： BAEDCDCBA 例3：已知：AD 、 AE 分别为ABC的内、外角平分线， M 为 DE 的中点，求证：22ABBMACCM MED CBA 解析： 题型 3：2abc型结论的证明 例1：如图，直角ABC中， ABAC， ADBC，证明：2ABBD BC，2ACCD BC，2ADBD CD. 解析：...