4.5合并同类项 浙江省初一数学(上)全部课件整理 浙教版VIP免费

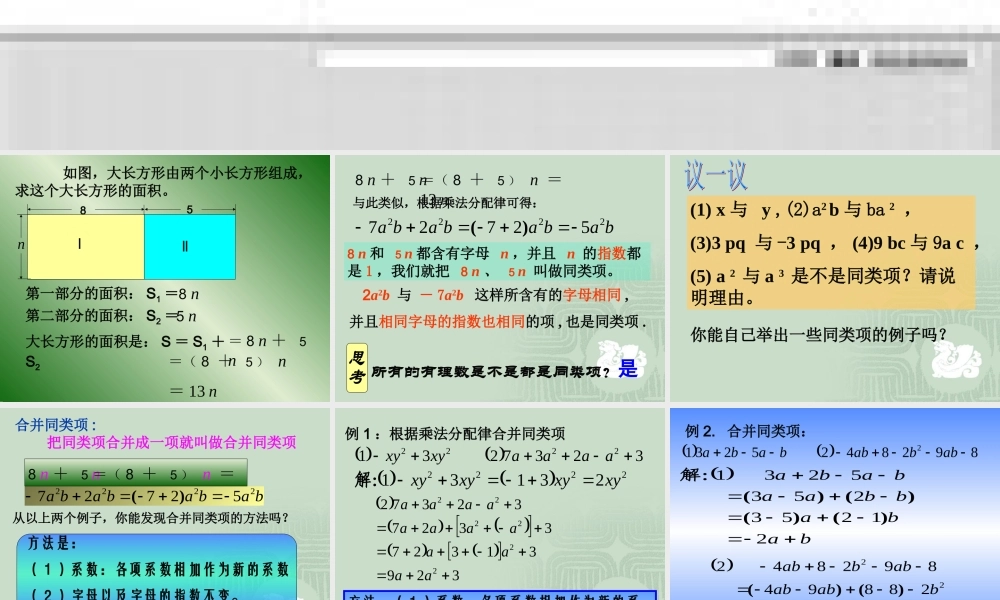
4.5 合并同类项 如图，大长方形由两个小长方形组成，求这个大长方形的面积。第一部分的面积： S1 ＝第二部分的面积： S2 ＝大长方形的面积是： S ＝ S1 ＋S28 n5 n＝ 8 n ＋ 5 n＝（ 8 ＋ 5 ） n＝ 13 n85nⅠⅡ8 n ＋ 5 n＝（ 8 ＋ 5 ） n ＝13 n8 n 和 5 n 都含有字母 n ，并且 n 的指数都是 1 ，我们就把 8 n 、 5 n 叫做同类项。与此类似，根据乘法分配律可得：babababa222252727)( 2a2b 与 － 7a2b 这样所含有的字母相同 , 并且相同字母的指数也相同的项 , 也是同类项 .所有的有理数是不是都是同类项？是 (1) x 与 y ,(2)a2 b 与 ba 2 ，(3)3 pq 与 -3 pq ， (4)9 bc 与 9a c ，(5) a 2 与 a 3 是不是同类项？请说明理由。你能自己举出一些同类项的例子吗？ 合并同类项 : 把同类项合并成一项就叫做合并同类项8 n ＋ 5 n＝（ 8 ＋ 5 ） n ＝13 nbabababa222252727)(从以上两个例子，你能发现合并同类项的方法吗？方法是：（ 1 ）系数：各项系数相加作为新的系数（ 2 ）字母以及字母的指数不变。你能举例说明吗？试试看，并与你的同伴交流。 例 1 ：根据乘法分配律合并同类项  32372312222aaaaxyxy 222223131xyxyxyxy解： 32931327332732372222222aaaaaaaaaaaa方法：（ 1 ）系数：各项系数相加作为新的系数 （ 2 ）字母以及字母的指数不变。 例 2. 合并同类项：  89284252312abbabbaba bababbaababa212532535231)()()()(解： 222221329428894892842babbabbabababbab)()()( 例 . 求多项式 2a2b-3a-3a2b+2a 的值 ,已知 a=-0.5,b=4解： 2a2b-3a-3a2b+2a = 2a2b-32b-3a+2a =(2-3)a2b+(-3+2)a =-a2b-a 当 a=-0.5,b=4 时，原式 =-(-0.5)2×4 － (-0.5) =-0.25×4+0.5 =-1+0.5=-0.5先化简，后求值 通过以上的练习你可以找出合并同类项的要点是什么？ 一变一不变一变就是系数要变（新系数变为原来各系数的代数和）一不变就是字母和字母的指数不变 （原来的字母和字母的指数照抄） 思考题： 一家商店以每 a 包元的价格买进了 30 包甲种绿茶...