4.1向量的概念与线性运算 届高三数学一轮复习精品课件第四章平面向量人教版 届高三数学一轮复习精品课件第四章平面向量人教版VIP免费

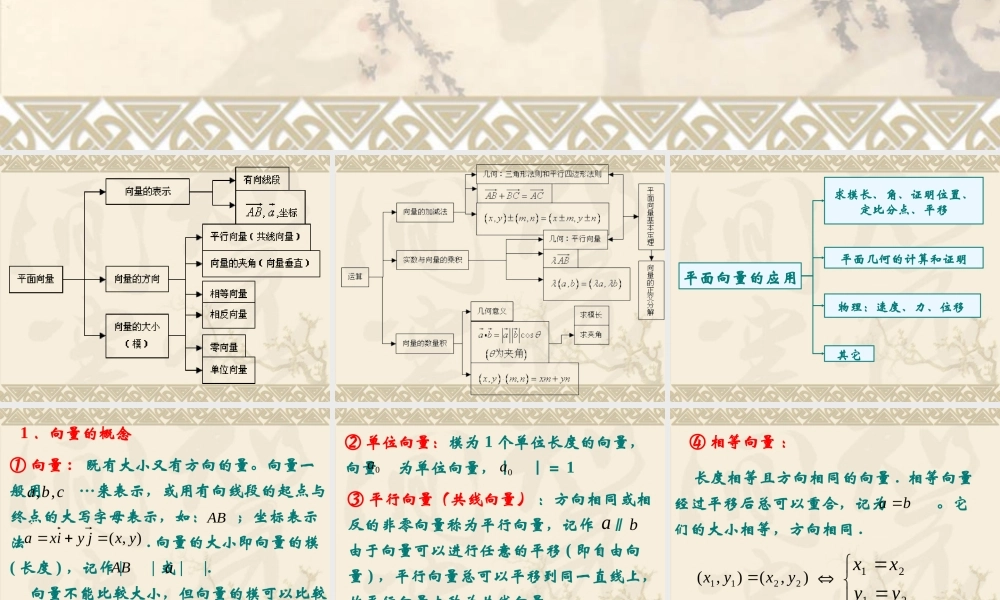
中国人民大学附属中学4.1 向量的概念与线性运算 平面向量的应用求模长、角、证明位置、定比分点、平移平面几何的计算和证明物理：速度、力、位移 其它 1 ．向量的概念① 向量 : 既有大小又有方向的量。向量一般用 …来表示，或用有向线段的起点与终点的大写字母表示，如： ；坐标表示法 . 向量的大小即向量的模( 长度 ) ，记作 | | 或 | |. 向量不能比较大小，但向量的模可以比较大小 cba,,AB�),(yxjyixaAB�a ② 单位向量：模为 1 个单位长度的向量，向量 为单位向量，｜ ｜＝ 1 0a0a③ 平行向量（共线向量） ：方向相同或相反的非零向量称为平行向量，记作 ∥ 由于向量可以进行任意的平移 ( 即自由向量 ) ，平行向量总可以平移到同一直线上，故平行向量也称为共线向量。 ab ④ 相等向量 ： 长度相等且方向相同的向量 . 相等向量经过平移后总可以重合，记为 。它们的大小相等，方向相同 . ba ),(),(2211yxyx2121yyxx 2 ．向量的运算（ 1 ）向量加法 : 向量加法的“三角形法则”与“平行四边形法则”① 用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量 . ② 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点 . 向量加法的三角形法则可推广至多个向量相加 （ 2 ）向量的减法 求两个向量差的运算，叫做向量的减法 .向量 加上 的相反向量叫做 与 的差 . abba)( baba（ 3 ）实数与向量的积 实数 λ 与向量 的积是一个向量，记作λ ，它的长度与方向规定如下： aa ①aa② 当 λ>0 时， λ 的方向与 的方向相同 ;当 λ<0 时， λ 的方向与 的方向相反；当 λ=0 时， ，方向是任意的 . aaaa0 a3 ．两个向量共线定理 向量 与非零向量 共线，等价于有且只有一个实数 λ ，使得 =λ bbaa 4 ．平面向量的基本定理 如果 是一个平面内的两个不共线向量，那么对这一平面内的任一向量 ，有且只有一对实数 使： . 其中不共线的向量 叫做表示这一平面内所有向量的一组基底 21,ee a21,2211eea...