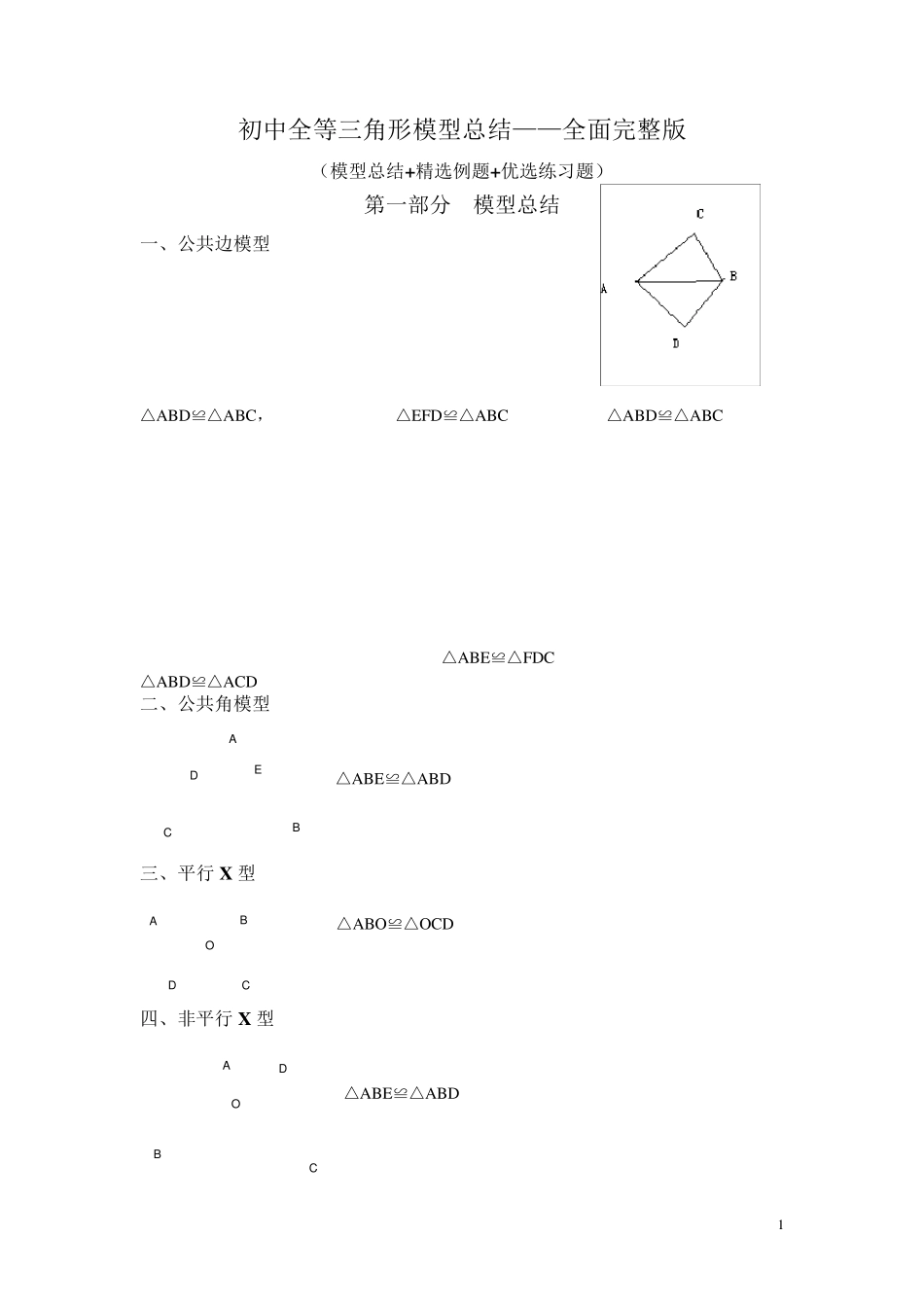
1 初中全等三角形模型总结——全面完整版 (模型总结+精选例题+优选练习题) 第一部分 模型总结 一、公共边模型 △ABD≌△ABC, △EFD≌△ABC △ABD≌△ABC △ABE≌△FDC △ABD≌△ACD 二、公共角模型 △ABE≌△ABD 三、平行 X 型 △ABO ≌△O CD 四、非平行 X 型 △ABE≌△ABD ACBEDOABDCOABCD 2 五、母子等腰三角形 △ABD≌△AEC ,△ABE≌△ACD 六、旋转模型 图1 △ ABC≌△AB`C 第二部分 精选例题 例 1.如图,已知AB∥CD,AD∥BC,F 在DC 的延长线上,AM=CF,FM 交DA 的延长线上于E.交BC 于N,求证:AE=CN. 思路分析:欲证AE=CN.看它们在哪两个三角形中, 设法证这两个三角形全等即可.结合图形可发现 △AME≌△FCN 可证. 题设告知AM=CF,AD∥BC,AB∥CD.由两平行条件, 可找两对角相等. ∠1=∠2(对顶角相等) ∴∠2=∠E(等量代换) ∴AE=CN (全等三角形的对应边相等) 例 2.△ABC 中,∠ACB=90°,AC=BC,过 C 的一条直线CE⊥AE 于E,BD⊥CE 的延长线于D,求证:AE=BD+DE. 思路分析:从本例的结论知是求线段和的问题, 由此入手,很难找到突破口.此时可迅速调整思维角 度,可仔细观察图形,正确的图形是证题的“向导”,由 此可发现△ACE 与△CBD 好像(猜测)全等.那么 AE=CD=CE+DE.又 BD=CE.那么,此时已水落石出. BCAEDC'B'ABCC'B'BAC 3 AC=BC (已知) ∠1=∠3 (已证) ∠AEC=∠CDB(已证) ∴△ACE≌△CBD(AAS) ∴BD=CE,AE=CD(全等三角形的对应边相等) AE=CE=CE+DE ∴AE=BD+DE(等量代换) 例 3.如图,AD 是△ABC 的中线,DE,DF 分别平分∠ADB 和∠ADC,连接EF,求证:EF